(本小题满分12分)已知等差数列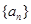 的公差大于0,且
的公差大于0,且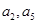 是方程
是方程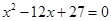 的两根,数列
的两根,数列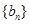 的前
的前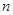 项的和为
项的和为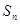 ,且
,且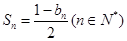 .
.
(1)求数列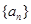 ,
,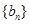 的通项公式;
的通项公式;
(2)若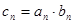 ,设数列
,设数列 的前
的前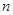 项和
项和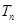 ,证明:
,证明: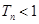 .
.
某电器商经过多年的经验发现本店每个月售出的电冰箱的台数ξ是一个随机变量,它的分布列为P(ξ=i)= (i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?
(i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?
一盒中装有零件12个,其中有9个正品,3个次品,从中任取一个,如果每次取出次品就不再放回去,再取一个零件,直到取得正品为止.求在取得正品之前已取出次品数的期望.
某工艺厂开发一种新工艺品,头两天试制中,该厂要求每位师傅每天制作10件,该厂质检部每天从每位师傅制作的10件产品中随机抽取4件进行检查,若发现有次品,则当天该师傅的产品不能通过.已知李师傅第一天、第二天制作的工艺品中分别有2件、1件次品.
(1)求两天中李师傅的产品全部通过检查的概率;
(2)若厂内对师傅们制作的工艺品采用记分制,两天全不通过检查得0分,通过1天、2天分别得1分、2分,求李师傅在这两天内得分的数学期望.
甲、乙两射手在同一条件下进行射击,分布列如下:射手甲击中环数8,9,10的概率分别为0.2,0.6,0.2;射手乙击中环数8,9,10的概率分别为0.4,0.2,0.4.用击中环数的期望与方差比较两名射手的射击水平.
已知离散型随机变量ξ1的概率分布为
| ξ1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| P |
 |
 |
 |
 |
 |
 |
 |
离散型随机变量ξ2的概率分布为
| ξ2 |
3.7 |
3.8 |
3.9 |
4 |
4.1 |
4.2 |
4.3 |
| P |
 |
 |
 |
 |
 |
 |
 |
求这两个随机变量数学期望、方差与标准差.