(本小题满分12分)随着教育改革的不断深入,各学校加大对学生综合素质的培养,为了丰富同学们的课余生活,某重点中学结合学校实际开展了诸多社团活动,为更好地开展社团活动,学校计划成立社团活动指导小组,想从“航模”,“乒乓球”,“声乐”,“社交礼仪”四个社团中利用分层抽样的方法抽取若干人组成校社团指导小组,有关数据见下表(单位:人)
| 社团 |
相关人数 |
抽取人数 |
| 航模 |
32 |
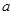 |
| 乒乓球 |
24 |
3 |
| 声乐 |
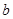 |
5 |
| 社交礼仪 |
16 |
 |
(Ⅰ)求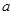 ,
,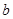 ,
, 的值;
的值;
(Ⅱ)若从“航模”与“社交礼仪”社团已抽取的人中选2人担任指导小组组长,求这2人分别来自这两个社团的概率.
设向量 ,过定点
,过定点 ,以
,以 方向向量的直线与经过点
方向向量的直线与经过点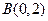 ,以向量
,以向量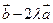 为方向向量的直线相交于点P,其中
为方向向量的直线相交于点P,其中
(1)求点P的轨迹C的方程;
(2)设过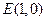 的直线
的直线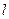 与C交于两个不同点M、N,求
与C交于两个不同点M、N,求 的取值范围
的取值范围
已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4、且位于x轴上方的点,A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M.
(1)求抛物线方程;
(2)过M作MN⊥FA,垂足为N,求点N的坐标。
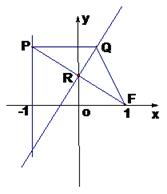
在平面直角坐标系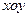 中,设点
中,设点 (1,0),直线
(1,0),直线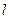 :
: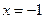 ,点
,点 在直线
在直线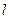 上移动,
上移动, 是线段
是线段 与
与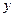 轴的交点,
轴的交点, 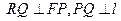 .
.
(Ⅰ)求动点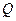 的轨迹的方程;
的轨迹的方程;
(Ⅱ) 记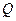 的轨迹的方程为
的轨迹的方程为 ,过点
,过点 作两条互相垂直的曲线
作两条互相垂直的曲线 的弦
的弦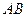 、
、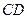 ,设
,设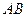 、
、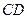 的中点分别为
的中点分别为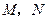 .求证:直线
.求证:直线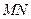 必过定点
必过定点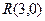 .
.
已知椭圆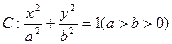 的离心率为
的离心率为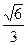 ,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且
,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且 ,定点A(-4,0).
,定点A(-4,0).
(1)求证:当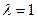 时.,
时.,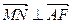 ;
;
(2)若当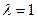 时有
时有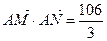 ,求椭圆C的方程;
,求椭圆C的方程;
(3)在(2)的条件下,当M、N两点在椭圆C运动时,当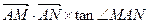 的值为6
的值为6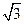 时, 求出直线MN的方程.
时, 求出直线MN的方程.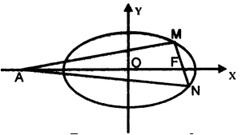
设直线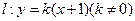 与椭圆
与椭圆 相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
(1)证明: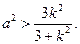 ;
;
(2)若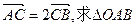 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.