(本小题满分13分)设函数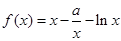 .
.
(Ⅰ)若函数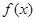 在定义域上为增函数,求实数
在定义域上为增函数,求实数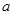 的取值范围;
的取值范围;
(Ⅱ)求函数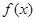 的极值点.
的极值点.
如图,在四棱锥 中,
中,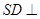 底面
底面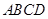 ,底面
,底面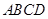 是平行四边形,
是平行四边形,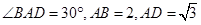 ,
,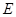 是
是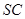 的中点。
的中点。
(1)求证: ;
;
(2)求证: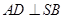 ;
;
(3)若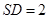 ,求二面角
,求二面角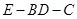 的余弦值.
的余弦值.
已知以角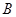 为钝角的
为钝角的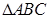 的内角
的内角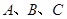 的对边分别为
的对边分别为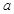 、
、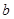 、
、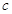 ,
,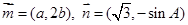 ,且
,且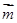 与
与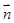 垂直。
垂直。
(1)求角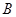 的大小;
的大小;
(2)求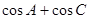 的取值范围.
的取值范围.
在某次测验中,有6位同学的平均成绩为75分.用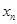 表示编号为
表示编号为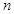 (
( )的同学所得成绩,且前5位同学的成绩如下:70,76,72,70,72.
)的同学所得成绩,且前5位同学的成绩如下:70,76,72,70,72.
(1)求第6位同学的成绩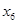 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差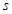 ;
;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
已知数列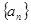 是等差数列,且
是等差数列,且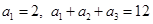 .
.
(1)求数列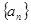 的通项公式;(2)令
的通项公式;(2)令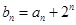 ,求数列
,求数列 前n项和
前n项和 .
.
已知函数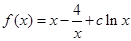 ,其中
,其中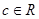 ,
,
(1)当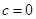 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)讨论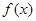 的单调性;
的单调性;
(3)若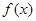 有两个极值点
有两个极值点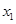 和
和 ,记过点
,记过点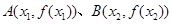 的直线的斜率为
的直线的斜率为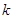 ,问是否存在
,问是否存在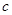 ,使得
,使得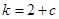 ?若存在,求出
?若存在,求出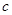 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.