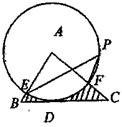
如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是。(结果保留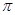 )
)
某种规格小纸杯的侧面是由一半径为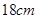 、圆心角是
、圆心角是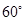 的扇形
的扇形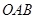 剪去一半径
剪去一半径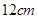 的同心圆扇形
的同心圆扇形 所围成的(不计接缝)(如图1).
所围成的(不计接缝)(如图1).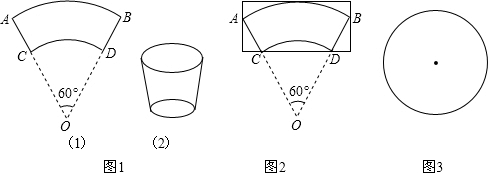
(1)求纸杯的底面半径和侧面积(结果保留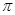 );
);
(2)要制作这样的纸杯侧面,如果按照图2所示的方式剪裁(不允许有拼接),至少要用多大的矩形纸片?
(3)如图3,若在一张半径为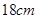 的圆形纸片上剪裁这样的纸杯侧面(不允许有拼接),最多能裁出多少个?
的圆形纸片上剪裁这样的纸杯侧面(不允许有拼接),最多能裁出多少个?
机械加工需要用油进行润滑以减小摩擦,某企业加工一台大型机械设备润滑用油量为90千克,用油的重复利用率为60%,按此计算,加工一台大型机械设备的实际耗油量为36千克,为了建设节约型社会,减少油耗,该企业的甲、乙两个车间都组织了人员为减少实际耗油量进行攻关.(1)甲车间通过技术革新后,加工一台大型机械设备润滑用油量下降到70千克,用油量的重复利用率仍然为60%.问甲车间技术革新后,加工一台大型机械设备的实际耗油量是多少千克?
(2)乙车间通过技术革新后,不仅降低了润滑用油量,同时也提高了用油的重复利用率,并且发现在技术革新前的基础上,润滑用油量每减少1千克,用油的重复利用率将增加1.6%,这样乙车间加工一台大型机械设备的实际耗油量下降到12千克,问乙车间技术革新后,加工一台大型机械设备的润滑用油量是多少千克?用油的重复利用率是多少?
如图,在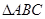 中,
中,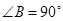 ,点
,点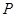 从点
从点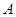 开始沿
开始沿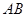 边向点
边向点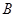 以
以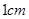 /秒的速度移动,点
/秒的速度移动,点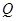 从点
从点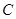 开始沿
开始沿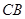 边向点
边向点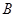 以
以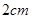 /秒的速度移动.
/秒的速度移动. 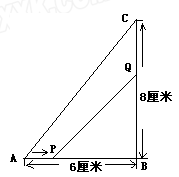
(1)如果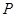 、
、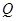 分别从
分别从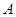 、
、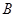 同时出发,几秒后
同时出发,几秒后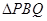 是等腰三角形?
是等腰三角形?
(2)如果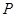 、
、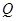 分别从
分别从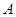 、
、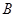 同时出发,几秒后
同时出发,几秒后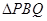 的面积等于
的面积等于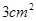 ?
?
(3)如果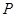 、
、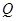 分别从
分别从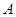 、
、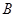 同时出发,四边形
同时出发,四边形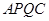 的面积是
的面积是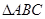 面积的三分之二?
面积的三分之二?
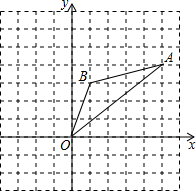
如图,在边长为1的正方形组成的网格中,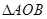 的顶点均在格点上,其中点
的顶点均在格点上,其中点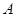 (5,4),
(5,4),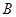 (1,3),将
(1,3),将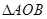 绕点
绕点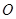 逆时针旋转
逆时针旋转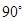 后得到
后得到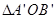 .
.
(1)画出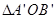 ;
;
(2)在旋转过程中点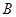 所经过的路径长为___________.
所经过的路径长为___________.
(3)求在旋转过程中线段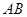 、
、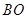 扫过的图形的面积之和.
扫过的图形的面积之和.
如图,在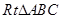 中,
中,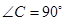 ,
,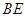 平分
平分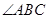 交
交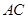 于点
于点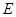 ,点
,点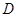 在
在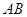 边上且
边上且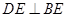 .
. 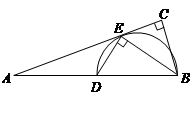
(1)判断直线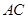 与
与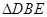 外接圆的位置关系,并说明理由;
外接圆的位置关系,并说明理由;
(2)若 ,
,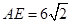 ,求
,求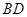 的长.
的长.