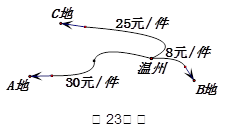如图，抛物线y＝－x2＋bx＋c与x轴交于A、B两点，与y轴交于点C，点O为坐标原点，点D为抛物线的顶点，点E在抛物线上，点F在x轴上，四边形OCEF为矩形，且OF＝2，EF＝3。
（1）求抛物线所对应的函数解析式；
（2）求△ABD的面积；
（3）将△AOC绕点C逆时针旋转90°，点A对应点为点G，问点G是否在该抛物线上？请说明理由。
2008年5月12日14时28分在我国四川省汶川地区发生了里氏8.0级强烈地震，灾情牵动全国人民的心，“一方有难、八方支援”．某厂计划加工1500顶帐篷支援灾区人民，在加工了300顶帐篷后，由于救灾需要工作效率提高到原来的1.5倍，结果提前4天完成了任务．求原来每天加工多少顶帐篷？
在一个可以改变体积的容器内有一定质量的二氧化碳气体，当改变容器的体积时，气体的密度也会随之改变，密度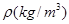
与体积
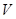
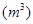之间的函数关系如图所示，。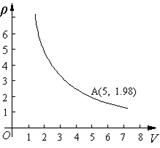
（1）通过图象你能得到什么信息（至少写一条）？
（2）写出
与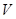之间函数关系式；
(3）求当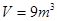
时，二氧化碳的密度。
先化简代数式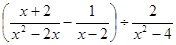
，请你取一个
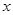的值，求出此时代数式的值．
如图，经过原点的抛物线
与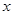
轴的另一个交点为A.过点
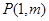作直线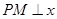
轴于点M，交抛物线于点B.记点B关于抛物线对称轴的对称点为C（B、C不重合）.连结CB,CP。当
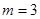时，求点A的坐标及BC的长；当
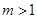时，连结CA，问
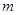为何值时
？过点P作
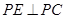且
，问是否存在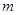，使得点E落在坐标轴上？若存在，求出所有满足要求的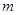的值，并定出相对应的点E坐标；若不存在，请说明理由。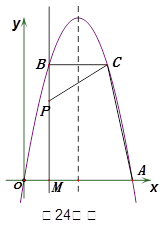
温州享有“中国笔都”之称，其产品畅销全球，某制笔企业欲将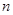
件产品运往A,B,C三地销售，要求运往C地的件数是运往A地件数的2倍，各地的运费如图所示。设安排
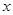件产品运往A地。当
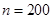时①根据信息填表：
| A地 |
B地 |
C地 |
合计 |
|
| 产品件数（件） |
|
 |
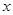200 |
|
| 运费（元） |
30 |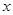
②若运往B地的件数不多于运往C地的件数，总运费不超过4000元，则有哪几种运输方案？若总运费为5800元，求
的最小值。