已知向量 =
= 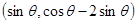 ,
, =(1,2)
=(1,2)
(1)若 ∥
∥  ,求tan
,求tan 的值。
的值。
(2)若| |=
|=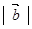
 ,
, ,求
,求 的值
的值
第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行 ,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”。
(1)如果用分层抽样的方法从“高个子”和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是 “高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望。
的数学期望。
在极坐标系中,从极点O作直线与另一直线 相交于点M,在OM上取一点P,使
相交于点M,在OM上取一点P,使 .
.
(1)求点P的轨迹方程; (2)设R为
(2)设R为 上任意一点,试求RP的最小值.
上任意一点,试求RP的最小值.
已知函数 =
= +
+ 有如下性质:如果常数
有如下性质:如果常数 >0,那么该函数在
>0,那么该函数在 0,
0,
 上是减函数,在
上是减函数,在
 ,+∞
,+∞ 上是增函数.
上是增函数.
(Ⅰ)如果函数 =
= +
+ (
( >0)的值域为
>0)的值域为 6,+∞
6,+∞ ,求
,求 的值;
的值;
(Ⅱ)研究函数 =
= +
+ (常数
(常数 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;
(Ⅲ)对函数 =
= +
+ 和
和 =
= +
+ (常数
(常数 >0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数 (
( 是正整数)在区间[
是正整数)在区间[ ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论).
已知数列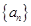 满足:
满足: =
= =2,
=2,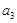 =3,
=3, =
=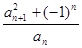 (
( ≥2)
≥2)
(Ⅰ)求: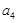 ,
, ,
,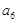 ;
;
(Ⅱ)是否存在实数 ,使得数列
,使得数列 (
( ∈N*)是等差数列?若存在,求出所有满足条件的
∈N*)是等差数列?若存在,求出所有满足条件的 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知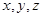 均为实数,且
均为实数,且
求证: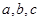 中至少有一个大于0
中至少有一个大于0