已知函数
(1)若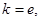 求函数
求函数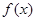 的单调区间;
的单调区间;
(2)若 且对任意
且对任意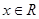 ,
, 恒成立,求实数
恒成立,求实数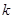 的取值范围;
的取值范围;
(3)设函数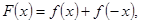 求证:
求证: .
.
设定义在 上的函数
上的函数 满足:对任意
满足:对任意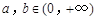 ,都有
,都有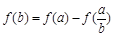 ,且当
,且当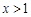 时,
时,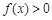 .
.
⑴求 的值;
的值;
⑵判断并证明函数 的单调性;
的单调性;
⑶如果 ,解不等式
,解不等式 .
.
函数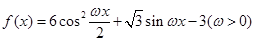 在一个周期内的图象如图所示,
在一个周期内的图象如图所示, 为图象的最高点,
为图象的最高点, 、
、 为图象与
为图象与 轴的交点,且
轴的交点,且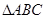 为正三角形。
为正三角形。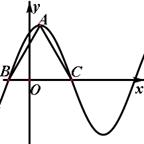
(Ⅰ)求 的值及函数
的值及函数 的值域;
的值域;
(Ⅱ)若 ,且
,且 ,求
,求 的值。
的值。
设平面内的向量 ,
, ,
, ,点
,点 是直线
是直线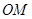 上的一个动点,且
上的一个动点,且 ,求
,求 的坐标及
的坐标及 的余弦值.
的余弦值.
在△ABC中,角A,B,C所对的边长分别是a,b,c.
(1)若sin C + sin(B-A)=" sin" 2A,试判断△ABC的形状;
(2)若△ABC的面积S = 3 ,且c =
,且c =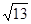 ,C =
,C = ,求a,b的值.
,求a,b的值.
已知与圆C:x2+y2-2x-2y+1=0相切的直线l交x轴,y轴于A,B两点,
OA|=a,|OB|=b(a>2,b>2).
(Ⅰ)求证:(a-2)(b-2)=2;
(Ⅱ)求线段AB中点的轨迹方程;
(Ⅲ)求△AOB面积的最小值.