(本小题满分12分)有7位歌手(1至7号)参加一场歌唱比赛,由500名大众评委现场投票决定歌手名次.根据年龄将大众评委分为五组,各组的人数如下:
| 组别 |
A |
B |
C |
D |
E |
| 人数 |
50 |
100 |
150 |
150 |
50 |
(1)为了调查评委对7位歌手的支持情况,现用分层抽样方法从各组中抽取若干评委,其中从B组抽取了6人,请将其余各组抽取的人数填入下表.
| 组别 |
A |
B |
C |
D |
E |
| 人数 |
50 |
100 |
150 |
150 |
50 |
| 抽取人数 |
|
6 |
|
|
|
(2)在(1)中,若A,B两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,求这2人都支持1号歌手的概率.
已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为 的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.(1)求椭圆C的标准方程;
的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.(1)求椭圆C的标准方程;
(2)若点P的坐标为(1,1),求证:直线PQ与圆 相切;
相切;
(3)试探究:当点P在圆O上运动时(不与A、B重合),直线PQ与圆O是否保持相切的位置关系?若是,请证明;若不是,请说明理由. 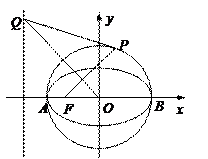
已知动圆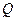 与
与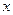 轴相切,且过点
轴相切,且过点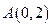 .
.
⑴求动圆圆心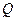 的轨迹
的轨迹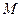 方程;
方程;
⑵设 、
、 为曲线
为曲线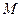 上两点,
上两点,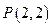 ,
, ,求点
,求点 横坐标的取值范围.
横坐标的取值范围.
解不等式: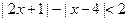
设数列 的各项都是正数,
的各项都是正数, ,
, ,
, .
.
⑴求数列 的通项公式;⑵求数列
的通项公式;⑵求数列 的通项公式;
的通项公式;
⑶求证: .
.
设函数 ,
, .
.
⑴当 时,求函数
时,求函数 图象上的点到直线
图象上的点到直线 距离的最小值;
距离的最小值;
⑵是否存在正实数 ,使
,使 对一切正实数
对一切正实数 都成立?若存在,求出
都成立?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.