(本小题满分14分)已知双曲线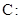
 (
( ,
, ),
), 、
、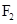 分别是它的左、右焦点,
分别是它的左、右焦点, 是其左顶点,且双曲线的离心率为
是其左顶点,且双曲线的离心率为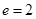 .设过右焦点
.设过右焦点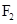 的直线
的直线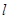 与双曲线
与双曲线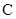 的右支交于
的右支交于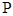 、
、 两点,其中点
两点,其中点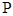 位于第一象限内.
位于第一象限内.
(1)求双曲线的方程;
(2)若直线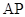 、
、 分别与直线
分别与直线 交于
交于 、
、 两点,求证:
两点,求证: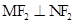 ;
;
(3)是否存在常数 ,使得
,使得 恒成立?若存在,求出
恒成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
.
四、附加题(本题10分,记入总分)
23.若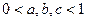 ,且
,且 满足
满足 ,求
,求
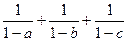 的最小值.
的最小值.
.已知数列 的前
的前 项和为
项和为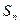 ,且对于任意
,且对于任意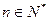 ,都有
,都有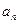 是
是 与
与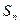 的等差中项,
的等差中项,
(1)求证: ;
;
(2)求证: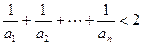 .
.
..如图,某小区准备在一直角围墙 内的空地上植造“绿地
内的空地上植造“绿地 ”,其中
”,其中 ,
,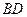 长可根据需要进行调节(
长可根据需要进行调节(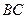 足够长),现规划在
足够长),现规划在 内接正方形
内接正方形 内种花,其余地方种草,设种草的面积
内种花,其余地方种草,设种草的面积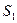 与种花的面积
与种花的面积 的比
的比 为
为 ,
,
(1)设角 ,将
,将 表示成
表示成 的函数关系;
的函数关系;
(2)当 为多长时,
为多长时, 有最小值,最小值是多少?
有最小值,最小值是多少?
.若果数列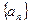 的项构成的新数列
的项构成的新数列 是公比为
是公比为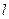 的等比数
的等比数 列,则相应的数列
列,则相应的数列 是公比为
是公比为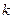 的等比数列,运用此性质,可以较为简洁的求出一类递推数列的通项公式,并简称此法为双等比数列法.已知数列
的等比数列,运用此性质,可以较为简洁的求出一类递推数列的通项公式,并简称此法为双等比数列法.已知数列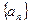 中,
中,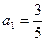 ,
, ,且
,且 .
.
(1)试利用双等比数列法求数列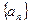 的通项公式;
的通项公式;
(2)求数列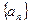 的前
的前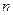 项和
项和
..已知函数 ,
,
(1)求函数 在
在 上的值域;
上的值域;
(2)在 中,若
中,若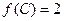 ,
, ,求
,求 .
.