小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.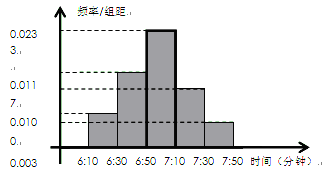
(1)根据图中的数据信息,求出众数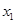 和中位数
和中位数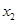 (精确到整数分钟);
(精确到整数分钟);
(2)小明的父亲上班离家的时间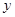 在上午
在上午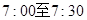 之间,而送报人每天在
之间,而送报人每天在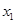 时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件
时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件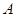 )的概率.
)的概率.
如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,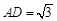 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.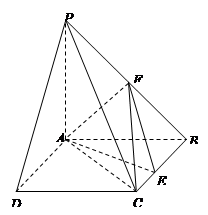
(1)若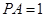 ,求证:
,求证: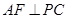 ;
;
(2)若二面角 的大小为
的大小为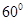 ,则CE为何值时,三棱锥
,则CE为何值时,三棱锥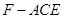 的体积为
的体积为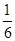 .
.
已知向量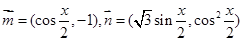 ,设函数
,设函数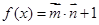 .
.
(1)求函数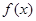 的单调递增区间;
的单调递增区间;
(2)在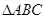 中,角
中,角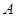 、
、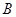 、
、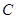 的对边分别为
的对边分别为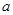 、
、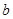 、
、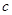 ,且满足
,且满足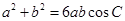 ,
,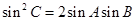 ,求
,求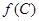 的值.
的值.
已知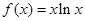 ,
,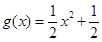 .
.
(1)设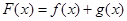 ,求函数
,求函数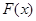 的图像在
的图像在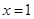 处的切线方程;
处的切线方程;
(2)求证: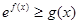 对任意的
对任意的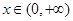 恒成立;
恒成立;
(3)若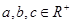 ,且
,且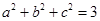 ,求证:
,求证: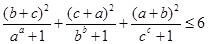 .
.
已知椭圆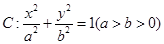 的离心率为
的离心率为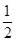 ,以原点为圆心、椭圆的短半轴长为半径的圆与直线
,以原点为圆心、椭圆的短半轴长为半径的圆与直线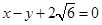 相切.
相切.
(1)求椭圆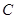 的方程;
的方程;
(2)设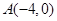 ,过点
,过点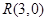 作与
作与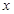 轴不重合的直线
轴不重合的直线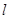 交椭圆于
交椭圆于 、
、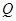 两点,连结
两点,连结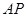 、
、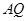 分别交直线
分别交直线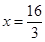 于
于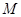 、
、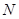 两点.试问直线
两点.试问直线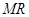 、
、 的斜率之积是否为定值,若是,求出该定值;若不是,请说明理由.
的斜率之积是否为定值,若是,求出该定值;若不是,请说明理由.