学校为了使运动员顺利参加运动会,招募了8名男志愿者和12名女志愿者,这20名志愿者的身高如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
| 男 |
|
女 |
||||||
| |
|
8 |
16 |
5 |
8 |
9 |
|
|
| 8 |
7 |
6 |
17 |
2 |
3 |
5 |
5 |
6 |
| 7 |
4 |
2 |
18 |
0 |
1 |
2 |
|
|
| |
|
1 |
19 |
0 |
|
|
|
|
(Ⅰ)用分层抽样的方法从“高个子”和“非高个子”中抽取5人,如果从这5人中随机选2人,那么至少有1人是“高个子”的概率是多少?
(Ⅱ)若从所有“高个子”中随机选3名志愿者,用 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望.
(本小题满分14分)
已知:对于数列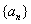 ,定义
,定义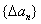 为数列
为数列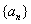 的一阶差分数列,其中
的一阶差分数列,其中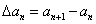 ,
,
(1)若数列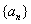 的通项公式
的通项公式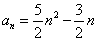 (
(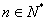 ),求:数列
),求:数列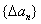 的通项公式;
的通项公式;
(2)若数列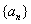 的首项是1,且满足
的首项是1,且满足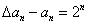 ,
,
①设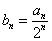 ,求证:数列
,求证:数列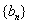 是等差数列,并求数列
是等差数列,并求数列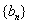 的通项公式;
的通项公式;
②求:数列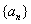 的通项公式及前
的通项公式及前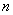 项和
项和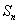
(本小题满分13分)
已知:向量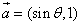 ,向量
,向量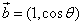 ,
,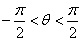 ,
,
(1)若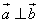 ,求:
,求: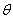 的值;
的值;
(2)求: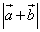 的最大值
的最大值
(本小题满分13分)
已知:定义在R上的函数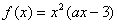 ,其中a为常数。
,其中a为常数。
(1)若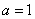 ,求:
,求: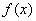 的图象在点
的图象在点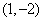 处的切线方程;
处的切线方程;
(2)若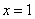 是函数
是函数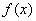 的一个极值点,求:实数a的值;
的一个极值点,求:实数a的值;
(3)若函数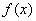 在区间
在区间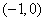 上是增函数,求:实数a的取值范围
上是增函数,求:实数a的取值范围
(本小题满分13分)
已知:若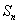 是公差不为0的等差数列
是公差不为0的等差数列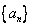 的前
的前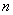 项和,且
项和,且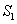 、
、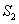 、
、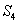 成等比数列。
成等比数列。
(1)求:数列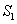 、
、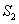 、
、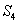 的公比;
的公比;
(2)若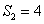 ,求:数列
,求:数列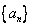 的通项公式
的通项公式
(本小题满分13分)
已知:函数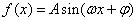 (其中
(其中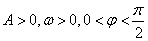 )的图象与
)的图象与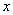 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为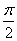 ,且图象上一个最低点为
,且图象上一个最低点为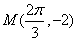
(1)求: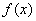 的解析式;
的解析式;
(2)当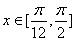 ,求:函数
,求:函数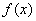 的值域
的值域