在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C: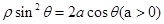 过点
过点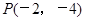 的直线
的直线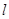 的参数方程为
的参数方程为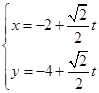 (t为参数),l与C分别交与M,N.
(t为参数),l与C分别交与M,N.
(1)写出C的平面直角坐标系方程和的普通方程;
(2)若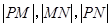 成等比数列,求a的值.
成等比数列,求a的值.
如图, 是棱长为
是棱长为 的正方体,
的正方体, 、
、 分别是棱
分别是棱 、
、 上的动点,且
上的动点,且 .
.
(1)求证: ;
;
(2)当 、
、 、
、 、
、 共面时,求:面
共面时,求:面 与面
与面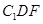 所成二面角的余弦值.
所成二面角的余弦值.
已知函数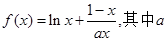 为大于零的常数。
为大于零的常数。
(1)若函数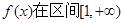 内调递增,求a的取值范围;
内调递增,求a的取值范围;
(2)求函数 在区间[1,2]上的最小值。
在区间[1,2]上的最小值。
已知数列{an}满足S n + a n= 2n +1.
(1)写出a1,a2,a3, 并推测a n的表达式;
(2)用数学归纳法证明所得的结论.
设复数 ,试求m取何值时
,试求m取何值时
(1)Z是实数;(2)Z是纯虚数;(3)Z对应的点位于复平面的第一象限
定义在[-1,1]上的奇函数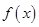 满足
满足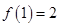 ,且当
,且当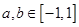 ,
, 时,有
时,有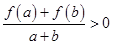 .
.
(1)试问函数f(x)的图象上是否存在两个不同的点A,B,使直线AB恰好与y轴垂直,若存在,求出A,B两点的坐标;若不存在,请说明理由并加以证明.
(2)若 对所有
对所有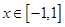 ,
,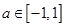 恒成立,
恒成立,
求实数m的取值范围.