(本小题满分10分)选修4-5;不等式选讲
若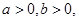 且
且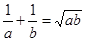
(1)求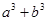 的最小值;
的最小值;
(2)是否存在 ,使得
,使得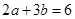 ?并说明理由.
?并说明理由.
(本题满分16分) 本题共有2个小题,第1小题满分10分,第2小题满分6分.
定义在R上的奇函数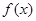 有最小正周期4,且
有最小正周期4,且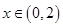 时,
时,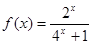
(1)判断并证明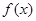 在
在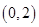 上的单调性,并求
上的单调性,并求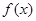 在
在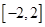 上的解析式;
上的解析式;
(2)当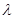 为何值时,关于
为何值时,关于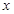 的方程
的方程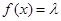 在
在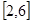 上有实数解?
上有实数解?
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
我们已经学习过如下知识:平面内到两个定点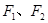 的距离和等于常数
的距离和等于常数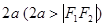 的点的轨迹叫做椭圆;平面内到两个定点
的点的轨迹叫做椭圆;平面内到两个定点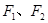 的距离之差的绝对值等于常数
的距离之差的绝对值等于常数 的点的轨迹叫做双曲线.
的点的轨迹叫做双曲线.
(1)试求平面内到两个定点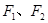 的距离之商为定值
的距离之商为定值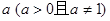 的点的轨迹;
的点的轨迹;
提示:取线段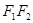 所在直线为
所在直线为 轴,线段
轴,线段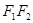 的垂直平分线为
的垂直平分线为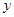 轴,建立直角坐标系,
轴,建立直角坐标系,
设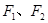 的坐标分别为
的坐标分别为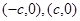 其中
其中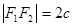
(2)若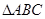 中,满足
中,满足 ,求三角形
,求三角形 的面积的最大值.
的面积的最大值.
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
在 中,角
中,角 、
、 、
、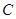 的对边分别
的对边分别 、
、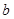 、
、 ,已知
,已知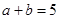 ,
, ,且
,且 .
.
(1)求角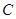 的大小;
的大小;
(2)求 的面积.
的面积.
(本题满分12分) 本题共有2个小题,第1小题满分6分,第2小题满分6分.
如图:三棱锥 中,
中, ^底面
^底面 ,若底面
,若底面 是边长为2的正三角形,且
是边长为2的正三角形,且
与底面 所成的角为
所成的角为 ,若
,若 是
是 的中点,
的中点,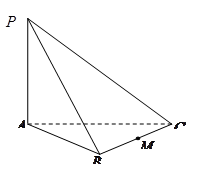
求:(1)三棱锥 的体积;
的体积;
(2)异面直线 与
与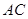 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
已知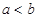 ,且
,且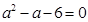 ,
, ,数列
,数列 、
、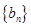 满足
满足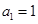 ,
, ,
, ,
,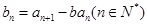 .
.
(1) 求证数列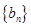 是等比数列;
是等比数列;
(2) (理科)求数列 的通项公式
的通项公式 ;
;
(3) (理科)若 满足
满足 ,
,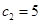 ,
, ,试用数学归纳法证明:
,试用数学归纳法证明: .
.