为丰富课余生活,某班开展了一次有奖知识竞赛,在竞赛后把成绩(满分为100分,分数均为整数)进行统计,制成如图的频率分布表:
(Ⅰ)求 的值;
的值;
(Ⅱ)若得分在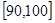 之间的有机会得一等奖,已知其中男女比例为2∶3,如果一等奖只有两名,写出所有可能的结果,并求获得一等奖的全部为女生的概率.
之间的有机会得一等奖,已知其中男女比例为2∶3,如果一等奖只有两名,写出所有可能的结果,并求获得一等奖的全部为女生的概率.
正△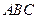 的边长为4,
的边长为4,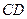 是
是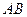 边上的高,
边上的高, 分别是
分别是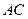 和
和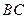 边的中点,现将△
边的中点,现将△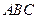 沿
沿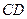 翻折成直二面角
翻折成直二面角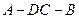 .
.
(1)试判断直线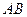 与平面
与平面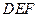 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求二面角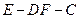 的余弦值;
的余弦值;
(3)在线段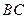 上是否存在一点
上是否存在一点 ,使
,使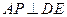 ?证明你的结论.
?证明你的结论.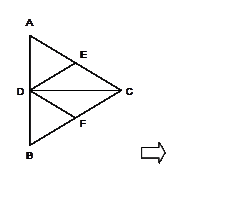

(12分)已知数列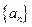 是各项均不为0的等差数列,
是各项均不为0的等差数列,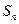 为其前
为其前 项和,且满足
项和,且满足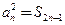 ,令
,令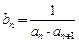 ,数列
,数列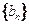 的前n项和为
的前n项和为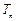 .
.
(Ⅰ)求数列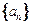 的通项公式及数列
的通项公式及数列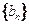 的前n项和
的前n项和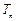 ;
;
(Ⅱ)是否存在正整数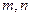
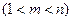 ,使得
,使得 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的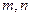 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(文)(本小题满分12分)
在某社区举办的《2008奥运知识有奖问答比赛》中,甲、乙、丙三人同时回答一道有关奥运知识的问题,已知甲回答对这道题的概率是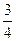 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是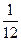 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是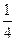 .
.
(1)求乙、丙两人各自回答对这道题的概率.
(2)求甲、乙、丙三人中恰有两人回答对该题的概率
(本小题满分12分)
从某学校高三年级共800名男生中随机抽取50名测量身高,测量发现被测学生身高全部介于155 cm和195 cm之间,将测量结果按如下方式分成八组:第一组[155,160)、第二组[160,165)、…、第八组[190,195],下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.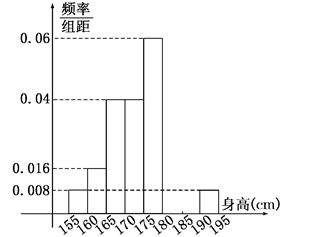
(1)估计这所学校高三年级全体男生身高180 cm以上(含180 cm)的人数;
(2)求第六组、第七组的频率并补充完整频率分布直方图;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为x、y,求满足|x-y|≤5的事件概率.
(理)(本小题满分12分)
为振兴旅游业,四川省2009年面向国内发行总量为2 000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡).某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游,其中是省外游客,其余是省内游客.在省外游客中有持金卡,在省内游客中有持银卡.
(1)在该团中随机采访2名游客,求恰有1人持银卡的概率;
(2)在该团中随机采访2名游客,求其中持金卡与持银卡人数相等的概率