好利来蛋糕店某种蛋糕每个成本为 元,每个售价为
元,每个售价为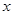 (
( )元,该蛋糕年销售量为
)元,该蛋糕年销售量为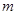 万个,若已知
万个,若已知 与
与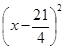 成正比,且售价为
成正比,且售价为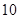 元时,年销售量为
元时,年销售量为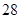 万个.
万个.
(1)求该蛋糕年销售利润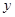 关于售价
关于售价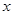 的函数关系式;
的函数关系式;
(2)求售价为多少时,该蛋糕的年利润最大,并求出最大年利润.
(本小题满分12分)
已知定点A(12,0),M为曲线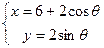 上的动点,(1)若
上的动点,(1)若 ,试求动点P的
,试求动点P的
轨迹C的方程.2)若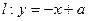 与曲线C相交于不同的两点E、F, O为坐标原点且
与曲线C相交于不同的两点E、F, O为坐标原点且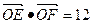 ,求∠EOF的余弦值和实数
,求∠EOF的余弦值和实数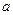 的值.
的值.
.(本小题满分12分).设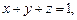 求
求 的最小值.
的最小值.
.(本小题满分12分)已知数列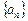 中,
中,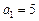 且
且 (
(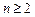 )。
)。
(1)求 ,
, 的值;
的值;
(2)设 ,是否存在实数
,是否存在实数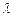 ,使数列
,使数列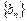 为等差数列,若存在请求其通项
为等差数列,若存在请求其通项 ,若不存在请说明理由。
,若不存在请说明理由。
(本小题满分12分)甲、乙两公司生产同一种产品,但由于设备陈旧,需要更新。经测算对于函数 、
、 及任意的
及任意的 ,当甲公司投放
,当甲公司投放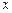 万元改造设备时,若乙公司投放改造设备费用小于
万元改造设备时,若乙公司投放改造设备费用小于 万元,则乙公司有倒闭的风险,否则无倒闭的风险;同样,当乙公司投入
万元,则乙公司有倒闭的风险,否则无倒闭的风险;同样,当乙公司投入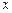 万元改造设备时,若甲公司投入改造设备费用小于
万元改造设备时,若甲公司投入改造设备费用小于 万元,则甲公司有倒闭的风险,否则无倒闭的风险。
万元,则甲公司有倒闭的风险,否则无倒闭的风险。
(1)请解释 、
、 的实际意义;
的实际意义;
(2)设 ,
, ,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无倒闭风险的情况下尽可能地减少改造设备资金。那么,甲、乙两公司至少各投入多少万元?
,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无倒闭风险的情况下尽可能地减少改造设备资金。那么,甲、乙两公司至少各投入多少万元?
本小题满分12分)如图所示,在四棱锥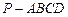 中,
中,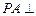 平面
平面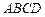 ,底面
,底面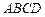 是直角梯形,
是直角梯形,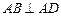 ,
,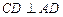 。
。
(1)求证:平面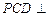 平面
平面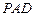 ;
;
(2)若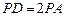 ,求二面角
,求二面角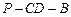 的大小。
的大小。