现有一个长、宽、高分别为5 dm、4 dm、3 dm的无盖长方体木箱（如图，AB＝5 dm，BC＝4 dm，AE＝3 dm）．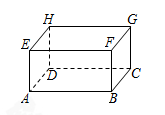
（1）求线段BG的长；
（2）现在箱外的点A处有一只蜘蛛，箱内的点G处有一只小虫正在午睡，保持不动．请你为蜘蛛设计一种捕虫方案，使得蜘蛛能以最短的路程捕捉到小虫．
（请计算说明，木板的厚度忽略不计）
如图，在边长为1的正方形网格内有一个三角形ABC
（1）把△ABC沿着
轴向右平移5个单位得到△A１B１C１，请你画出△A１B１C１
（2）请你以O点为位似中心在第一象限内画出△ABC的位似图形△A２B２C２，使得△ABC与△A２B２C２的位似比为1：2；
（3）请你写出△A２B２C２三个顶点的坐标。(3分)
若
，
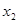是一元二次方程
的两根，不解方程，求
+
的值。
如图，△ABC中，
BC=6，求
及b、c。
如图，抛物线y=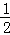
x2+mx+n交x轴于A、B两点，交y轴于点C，点P是它的顶点，点A的坐标是（1，0），点B的坐标是（﹣3，0）．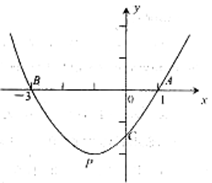
（1）求m、n的值；
（2）求直线PC的解析式．
[温馨提示：抛物线y=ax2+bx+c（a≠0）的顶点坐标为（﹣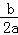
，
）]．
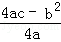如图，已知点E在△ABC的边AB上，∠C=90°，∠BAC的平分线交BC于点D，且D在以AE为直径的⊙O上．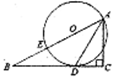
（1）求证：BC是⊙O的切线；
（2）已知∠B=30°，CD=4，求线段AB的长．