小王玩游戏:一张纸片,第一次将其撕成四小片,以后每次都将其中一片撕成更小的四片,如此进行下去。
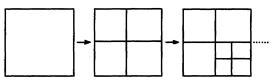
(1)填空:当小王撕了3次后,共有 张纸片;
(2)填空:当小王撕了n次后,共有 张纸片.(用含n的代数式表示)
(3)小王说:我撕了若干次后,共有纸片2013张,小王说的对不对?若不对,请说明你的理由;若对的,请指出小王需撕多少次?
中山市某施工队负责修建1800米的绿道.为了尽量减少施工对周边环境的影响,该队提高了施工效率,实际工作效率比原计划每天提高了20%,结果提前两天完成.求实际平均每天修绿道的长度?
“校园手机”现象越来越受到社会的关注,小记者刘凯随机调查了某校若干学生和家长对中学生带手机现象的看法,制作了如下的统计图: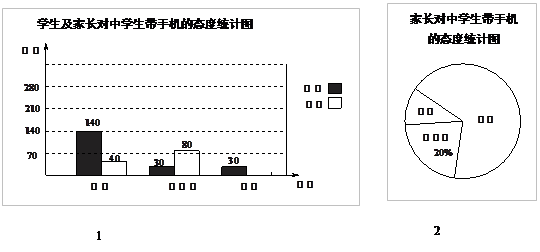
(1)求这次调查的总人数,并补全图1;
(2)求图2中表示家长“赞成”的圆心角的度数;
(3)针对随机调查的情况,刘凯决定从初三一班表示赞成的3位家长中随机选择2位进行深入调查,其中包含小亮和小丁的家长,请你利用树状图或列表的方法,求出小亮和小丁的家长被同时选中的概率.
如图,在边长均为1的小正方形网格纸中,△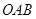 的顶点
的顶点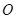 、
、 、
、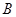 均在格点上,且
均在格点上,且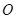 是直角坐标系的原点,点
是直角坐标系的原点,点 在
在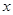 轴上.
轴上.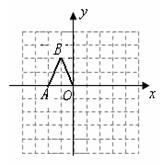
(1)以O为位似中心,将△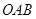 放大,使得放大后的△
放大,使得放大后的△ 与△
与△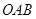 对应线段的比为2∶1,画出△
对应线段的比为2∶1,画出△ .(所画△
.(所画△ 与△
与△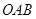 在原点两侧).
在原点两侧).
(2)求出线段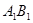 所在直线的函数关系式.
所在直线的函数关系式.
已知关于x的一元二次方程 (m -2)x2 + 2mx + m +3 =" 0" 有两个不相等的实数根.
(1)求m的取值范围; (2)当m取满足条件的最大整数时,求方程的根.
如图,在 ABCD中,
ABCD中,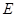 为
为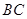 边上一点,且
边上一点,且 .
.
(1)求证: .
.
(2)若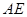 平分
平分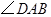 ,
,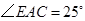 ,求
,求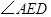 的度数.
的度数.