某批发公司批发某商品，每件商品进价80元，批发价120元，该批发商为鼓励经销商批发，决定当一次批发量超过100个时，每多批发一个，批发的全部商品的单价就降低0．04元，但最低批发价不能低于102元．
（1）当一次订购量为多少个时,每件商品的实际批发价为102元?
（2）当一次订购量为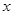
个, 每件商品的实际批发价为
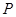元,写出函数
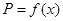的表达式；
（3）根据市场调查发现,经销商一次最大定购量为
个，则当经销商一次批发多少个零件时,该批发公司可获得最大利润．
在长方体ABCD－A1B1C1D1中，AB＝AD＝2，AA1＝a，E，F分别为AD，CD的中点.
（1）若AC1⊥D1F，求a的值；
（2）若a＝2，求二面角E－FD1－D的余弦值.
在平面直角坐标系xOy中，曲线y＝x2－2x－3与坐标轴的交点都在圆C上．
（1）求圆C的方程；
（2）若直线x＋y＋a＝0与圆C交于A，B两点，且AB＝2，求实数a的值．
已知m∈R，设p：复数z1＝(m－1)＋(m＋3)i (i是虚数单位)在复平面内对应的点在第二象限，q：复数z2＝1＋(m－2)i的模不超过
．
（1）当p为真命题时，求m的取值范围；
（2）若命题“p且q”为假命题，“p或q”为真命题，求m的取值范围．
已知函数
，
。
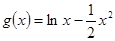（1）求函数
的解析式；
（2）若对于任意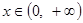
，都有
成立，求实数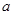
的取值范围；
（3）设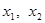
，
，且
，求证：
。
如图，已知点D（0，－2），过点D作抛物线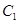
：
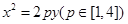的切线l,切点A在第二象限。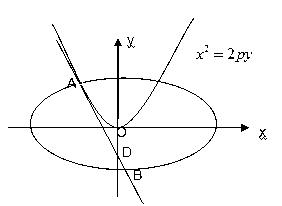
（1）求切点A的纵坐标；
（2）若离心率为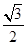
的椭圆
恰好经过A点，设切线l交椭圆的另一点为B，若设切线l,直线OA，OB的斜率为k,
,①试用斜率k表示
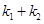②当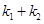取得最大值时求此时椭圆的方程。