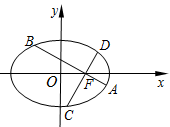
（本小题满分14分）如图，在平面直角坐标系
中，椭圆
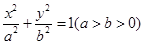的离心率为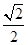
，过椭圆右焦点F作两条互相垂直的弦
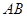和
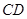，当直线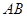斜率为0时，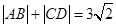
（1）求椭圆的方程；
（2）求由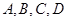
四点构成的四边形的面积的取值范围。
已知数列{an}的前n项和为Sn,且Sn=2n2+n,n∈N*,数列{bn}满足an=4log2bn+3,n∈N*.
(1)求an,bn;
(2)求数列{an·bn}的前n项和Tn.
设Sn为数列{an}的前n项和,已知a1≠0,2an-a1=S1·Sn,n∈N*.
(1)求a1,a2,并求数列{an}的通项公式;
(2)求数列{nan}的前n项和.
等差数列{an}中,a7=4,a19=2a9.
(1)求{an}的通项公式;
(2)设bn=
,求数列{bn}的前n项和Sn.
设数列{an}满足a1=2,a2+a4=8,且对任意n∈N*,函数f(x)=(an-an+1+an+2)x+an+1cos x-an+2sin x满足f′
=0.
(1)求数列{an}的通项公式;
(2)若bn=2(an+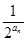
),求数列{bn}的前n项和Sn.
设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足
+
+…+
=1-
,n∈N* ,求{bn}的前n项和Tn.