(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线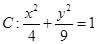 ,直线
,直线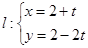 (
(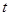 为参数)
为参数)
(1)写出曲线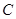 的参数方程,直线
的参数方程,直线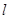 的普通方程;
的普通方程;
(2)过曲线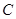 上任意一点
上任意一点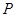 作与
作与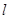 夹角为30°的直线,交
夹角为30°的直线,交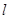 于点
于点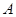 ,求
,求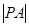 的最大值与最小值.
的最大值与最小值.
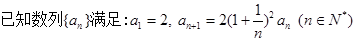
(1)求证:  是等比数列,并求出
是等比数列,并求出 的通项公式;
的通项公式;
(2) ,
, ,
, 
在平面直角坐标系 中,点
中,点 到两点
到两点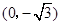 ,
, 的距离之和等于4,设点
的距离之和等于4,设点 的轨迹为
的轨迹为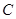 .
.
(Ⅰ)写出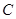 的方程;
的方程;
(Ⅱ)设直线 与
与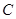 交于
交于 两点.k为何值时
两点.k为何值时

 ?此时
?此时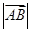 的值是多少?
的值是多少?
如图,在四棱锥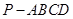 中,底面
中,底面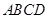 为直角梯形,且
为直角梯形,且 ,
,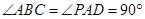 ,侧面
,侧面 底面
底面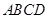 . 若
. 若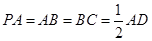 .
.
(Ⅰ)求证: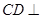 平面
平面 ;
;
(Ⅱ)侧棱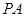 上是否存在点
上是否存在点 ,使得
,使得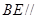 平面
平面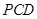 ?若存在,指出点
?若存在,指出点 的位置并证明,若不存在,请说明理由;
的位置并证明,若不存在,请说明理由;
(Ⅲ)求二面角 的余弦值.
的余弦值.
已知函数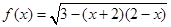 的定义域为
的定义域为 ,
, 的定义域为
的定义域为 .
.
(1)求 .
.
(2)记 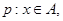
 ,若
,若 是
是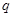 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围。
的取值范围。
在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2, ,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号n |
1 |
2 |
3 |
4 |
5 |
| 成绩xn |
70 |
76 |
72 |
70 |
72 |
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.