已知椭圆 过点
过点 ,且长轴长等于4.
,且长轴长等于4.
(1)求椭圆C的方程;
(2) 是椭圆C的两个焦点,圆O是以
是椭圆C的两个焦点,圆O是以 为直径的圆,直线
为直径的圆,直线 与圆O相切,并与椭圆C交于不同的两点A,B,若
与圆O相切,并与椭圆C交于不同的两点A,B,若 ,求
,求 的值.
的值.
在进行一项掷骰子放球游戏中,规定:若掷出1点,甲盒中放一球;若掷出2点或3点,乙盒中放一球;若掷出4点或5点或6点,丙盒中放一球,前后共掷3次,设 分别表示甲,乙,丙3个盒中的球数.
分别表示甲,乙,丙3个盒中的球数.
(Ⅰ)求 依次成公差大于0的等差数列的概率;
依次成公差大于0的等差数列的概率;
(Ⅱ)求随机变量z的概率分布列和数学期望.
已知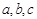 分别是
分别是 的角
的角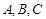 所对的边,且
所对的边,且 ,
, .
.
(Ⅰ)若 的面积等于
的面积等于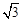 ,求
,求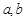 ;
;
(Ⅱ)若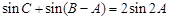 ,求
,求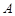 的值.
的值.
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
如图所示的“8”字形曲线是由两个关于 轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是
轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是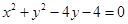 ,双曲线的左、右顶点
,双曲线的左、右顶点 、
、 是该圆与
是该圆与 轴的交点,双曲线与半圆相交于与
轴的交点,双曲线与半圆相交于与 轴平行的直径的两端点.
轴平行的直径的两端点.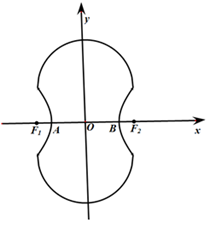
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为 、
、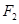 ,试在“8”字形 曲线上求点
,试在“8”字形 曲线上求点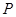 ,使得
,使得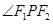 是直角.
是直角.
(3)过点 作直线
作直线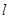 分别交“8”字形曲线中上、下两个半圆于点
分别交“8”字形曲线中上、下两个半圆于点 ,求
,求 的最大长度.
的最大长度.
(本题满分16分,第(1)小题7分,第(2)小题9分)
如图,在两块钢板上打孔,用钉帽呈半球形、钉身为圆柱形的铆钉(图1)穿在一起,在没有帽的一端锤打出一个帽,使得与钉帽的大小相等.铆合的两块钢板,成为某种钢结构的配件,其截面图如图2.(单位:mm,加工中不计损失).
(1)若钉身长度是钉帽高度的2倍,求铆钉的表面积;
(2)若每块钢板的厚度为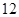 mm,求钉身的长度(结果精确到
mm,求钉身的长度(结果精确到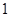 mm).
mm).
(本题满分14分,第(1)小题6分,第(2)小题8分)
如图,在四棱锥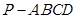 中,底面
中,底面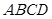 为矩形,
为矩形, 平面
平面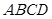 ,点
,点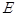 在线段
在线段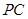 上,
上,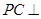 平面
平面 .
.
(1)求证: 平面
平面 ;
;
(2)若 ,
, ,求二面角
,求二面角 的大小.
的大小.