(本小题满分10分)已知 ,
, .
.
(1)求 和
和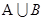 ;
;
(2)定义 且
且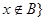 ,求
,求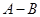 和
和 .
.
选修4-5:不等式选讲
已知函数 (a∈R).
(a∈R).
(1)当a=1时,求不等式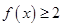 的解集;
的解集;
(2)若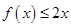 的解集包含
的解集包含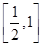 ,求a的取值范围.
,求a的取值范围.
选修4-4:坐标系与参数方程
在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立坐标系.已知点A的极坐标为 ,直线的极坐标方程为
,直线的极坐标方程为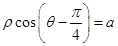 ,且点A在直线上.
,且点A在直线上.
(1)求a的值及直线的直角坐标方程;
(2)圆C的参数方程为 ,(α为参数),试判断直线与圆的位置关系.
,(α为参数),试判断直线与圆的位置关系.
选修4-1:几何证明选讲
如图 是
是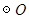 直径,
直径,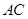 是
是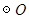 切线,
切线,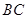 交
交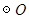 于点
于点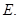

(1)若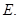 D为
D为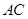 中点,求证:
中点,求证: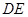 是
是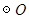 切线;
切线;
(2)若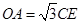 ,求
,求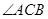 的大小.
的大小.
已知函数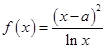 (其中a为常数).
(其中a为常数).
(1)当a=0时,求函数的单调区间;
(2)当0<a<1时,设函数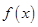 的3个极值点为
的3个极值点为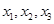 ,且
,且 .证明:
.证明: .
.
已知中心在原点 ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为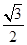 的椭圆过点
的椭圆过点

(1)求椭圆的方程;
(2)设不过原点 的直线
的直线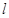 与该椭圆交于
与该椭圆交于 两点,满足直线
两点,满足直线 的斜率依次成等比数列,求
的斜率依次成等比数列,求 面积的取值范围.
面积的取值范围.