(本小题满分14分)如图,已知椭圆 的左焦点为F(
的左焦点为F( ,0),过点M(-3,0)作一条斜率大于0的直线
,0),过点M(-3,0)作一条斜率大于0的直线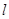 与椭圆W交于不同的两点A、B,延长BF交椭圆W于点C.
与椭圆W交于不同的两点A、B,延长BF交椭圆W于点C.
(1)求椭圆W的离心率;
(2)若∠MAC=60°,求直线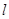 的斜率.
的斜率.
设椭圆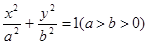 的左焦点为
的左焦点为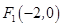 ,直线
,直线 与
与 轴交于点
轴交于点 ,过点
,过点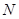 且倾斜角为30°的直线
且倾斜角为30°的直线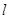 交椭圆于
交椭圆于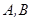 两点.
两点.
(Ⅰ)求直线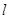 和椭圆的方程;
和椭圆的方程;
(Ⅱ)求证:点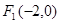 在以线段
在以线段 为直径的圆上;
为直径的圆上;
(Ⅲ)在直线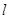 上有两个不重合的动点
上有两个不重合的动点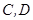 ,以
,以 为直径且过点
为直径且过点 的所有圆中,求面积最小的圆的半径长.
的所有圆中,求面积最小的圆的半径长.
已知三棱锥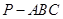 的三视图如图所示.
的三视图如图所示.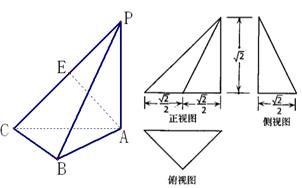
(Ⅰ)求证: 是直角三角形;
是直角三角形;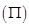 求三棱锥
求三棱锥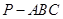 是全面积;
是全面积;
(Ⅲ)当点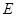 在线段
在线段 上何处时,
上何处时,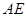 与平面
与平面 所成的角为
所成的角为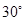 .
.
已知抛物线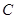 :
: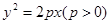 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.
(Ⅰ)求抛物线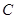 的方程;
的方程;
(Ⅱ)设直线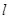 与抛物线
与抛物线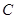 交于不同两点
交于不同两点 ,若满足
,若满足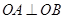 ,证明直线
,证明直线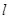 恒过定点,并求出定点
恒过定点,并求出定点 的坐标.
的坐标.
(Ⅲ)试把问题(Ⅱ)的结论推广到任意抛物线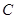 :
: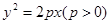 中,请写出结论,不用证明.
中,请写出结论,不用证明.
如图所示,平面 ⊥平面
⊥平面 ,
, ,
,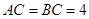 ,四边形
,四边形 是直角梯形,
是直角梯形,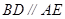 ,
,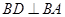 ,
, 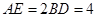 ,
, 分别为
分别为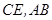 的中点.
的中点. 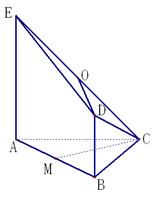
(Ⅰ) 用几何法证明: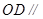 平面
平面 ;
;
(Ⅱ)用几何法证明: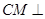 平面
平面 .
.
一个多面体的直观图与三视图如图所示, 分别是
分别是 中点
中点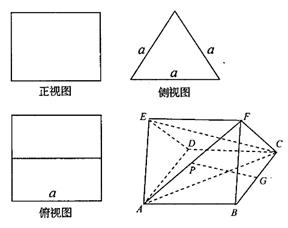
(Ⅰ)求此多面体的体积;
(Ⅱ)求证: .
.