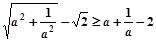(本小题12分)如图,在棱长均为4的三棱柱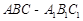 中,
中, 、
、 分别是
分别是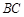 、
、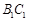 的中点
的中点
(1)求证: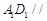 平面
平面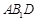 ;
;
(2)若平面ABC⊥平面BCC1B1,∠B1BC=60°,求三棱锥 的体积.
的体积.
(本小题满分12分)已知函数¦(x)=2―sin(2x+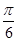 )―2sin2x,x∈[0,
)―2sin2x,x∈[0,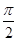 ]
]
(1)求函数¦(x)的值域;
(2)记△ABC的内角A、B、C所对的边长分别为a、b、c,若¦(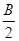 )=1,b=1,c=
)=1,b=1,c=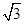 ,求a的值
,求a的值
已知x=1是函数f(x)=mx3-3(m+1)x2+nx+1的一个极值点,其中m,n∈R.
(1)求m与n的关系式;
(2)求f(x)的单调区间;
(3)当x∈[-1,1]时,m<0,函数y=f(x)的图象上任意一点的切线斜率恒大于3m,求m的取值范围.
(用数字表示结果)
某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选一题答一题的方式进行。每位选手最多有5次答题机会。选手累计答对3题或答错三题终止初赛的比赛。答对三题直接进入决赛,答错3题则被淘汰。已知选手甲连续两次答错的概率为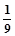 (已知甲回答每个问题的正确率相同,并且相互之间没有影响)
(已知甲回答每个问题的正确率相同,并且相互之间没有影响)
(1)求选手甲回答一个问题的正确率;
(2)求选手甲进入决赛的概率;
(3)设选手甲在初赛中答题个数为X,试写出X的分布列,并求甲在初赛中平均答题个数。
已知数列{an}满足a1= ,且前n项和Sn满足:Sn=n2an,求a2,a3,a4,猜想{an}的通项公式,并加以证明。
,且前n项和Sn满足:Sn=n2an,求a2,a3,a4,猜想{an}的通项公式,并加以证明。
已知a>0,求证: