(本题13分)已知函数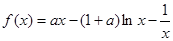 ,其中
,其中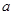 为实数.
为实数.
(1)求函数 的极大值点和极小值点;
的极大值点和极小值点;
(2)已知函数 的图象在
的图象在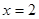 处的切线与
处的切线与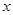 轴平行,
轴平行,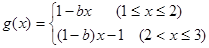 .且对任意
.且对任意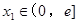 ,存在
,存在 ,使得
,使得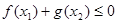 ,求实数
,求实数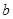 的最小值(其中
的最小值(其中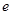 为自然对数的底数).
为自然对数的底数).
(本小题满分13分)
已知数列 满足:
满足: .
.
(1)求数列 的通项公式;
的通项公式;
(2)证明:
某通讯公司需要在三角形地带OAC区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域BOC内,乙中转站建在区域AOB内.分界线OB固定,且 百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°,设
百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°,设 百米,
百米, 百米.
百米.
(1)试将 表示成
表示成 的函数,并求出函数
的函数,并求出函数 的解析式;
的解析式;
(2)当 取何值时?整个中转站的占地面积
取何值时?整个中转站的占地面积 最小,并求出其面积的最小值.
最小,并求出其面积的最小值.
已知数列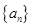 满足:
满足: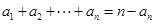 ,其中
,其中 .
.
(1)求证:数列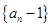 是等比数列;
是等比数列;
(2)令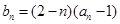 ,求数列
,求数列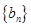 的最大项.
的最大项.
已知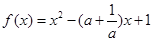 .
.
当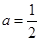 时,解不等式
时,解不等式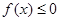 ;
;
(2)若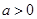 ,解关于
,解关于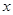 的不等式
的不等式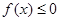 .
.
在△ABC中, 分别为内角A,B,C的对边,且
分别为内角A,B,C的对边,且
(1)求A的大小;
(2)若 ,试判断△ABC的形状.
,试判断△ABC的形状.