(本小题满分12分)如图,四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=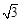 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.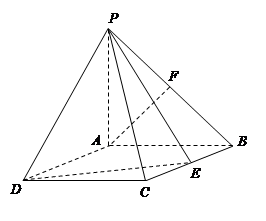
(Ⅰ)证明:无论点E在边BC的何处,都有PE⊥AF;
(Ⅱ)当BE为何值时,PA与平面PDE所成角的大小是45°?
(本小题满分13分)已知向量 ,
, ,函数
,函数

(1)求函数 的最小正周期及
的最小正周期及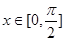 上的最值;
上的最值;
(2)若关于 的方程
的方程 在区间
在区间 上只有一个实根,求实数
上只有一个实根,求实数 的取值范围.
的取值范围.
(本小题满分12分)马航 牵动全球人的心,世界各国积极投身到马航的搜救工作中,了解海底构造是救援工作要做的第一件事.某搜救队在某海域的海平面上的同一条直线上的
牵动全球人的心,世界各国积极投身到马航的搜救工作中,了解海底构造是救援工作要做的第一件事.某搜救队在某海域的海平面上的同一条直线上的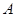 ,
,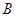 ,
,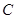 三点进行测量,得
三点进行测量,得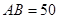 ,
,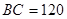 ,于
,于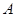 ,
,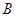 ,
,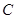 三处测得水深分别为
三处测得水深分别为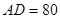 ,
,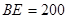 ,
,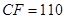 ,如图所示,试利用你所学知识求
,如图所示,试利用你所学知识求 的余弦值.
的余弦值.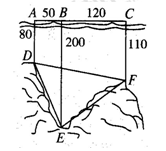
(本小题满分12分)已知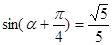 ,
,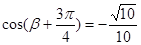 ,
,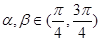 ,求
,求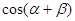 的值.
的值.
(本小题满分12分)在 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为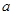 ,
, ,
, ,且
,且
(1)求角 的大小;
的大小;
(2)如果 ,
, ,求边长
,求边长 的值.
的值.
(本小题满分12分)设公差不等于零的等差数列 的前
的前 项和为
项和为 ,且
,且 ,
, ,
, ,
,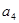 成等比数列
成等比数列
(1)求数列 的通项公式;
的通项公式;
(2)求 的值.
的值.