(本小题满分12分)在 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为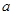 ,
, ,
, ,且
,且
(1)求角 的大小;
的大小;
(2)如果 ,
, ,求边长
,求边长 的值.
的值.
如图,在四棱锥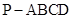 中,侧棱
中,侧棱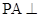 底面
底面 ,
,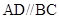 ,
, ,
,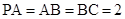 ,
,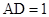 ,
, 是棱
是棱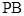 中点.
中点.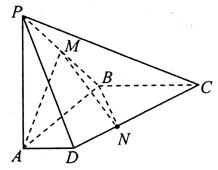
(1)求证: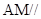 平面
平面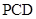 ;
;
(2)设点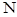 是线段
是线段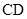 上一动点,且
上一动点,且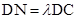 ,当直线
,当直线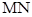 与平面
与平面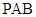 所成的角最大时,求
所成的角最大时,求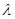 的值.
的值.
某市规定,高中学生三年在校期间参加不少于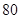 小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段
小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段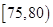 ,
, ,
,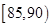 ,
,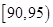 ,
, (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
(1)求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;
(2)从全市高中学生(人数很多)中任意选取3位学生,记 为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量
为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量 的分布列和数学期望
的分布列和数学期望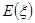 .
.
已知函数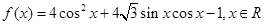 .
.
(1)求函数的最小正周期、最大值及取最大值时自变量的取值集合;
(2)在△ABC中,角A,B,C的对边分别是a,b,c;若a,b,c成等比数列,且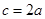 ,求
,求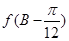 的值.
的值.
选修4—5:不等式选讲
设函数 .
.
(Ⅰ)解不等式 ;
;
(Ⅱ)若 ,使得
,使得 ,求实数
,求实数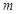 的取值范围.
的取值范围.
选修4—4:坐标系与参数方程
已知直线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程是
的极坐标方程是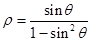 .
.
(1)写出直线 的极坐标方程与曲线
的极坐标方程与曲线 的普通方程;
的普通方程;
(2)若点 是曲线
是曲线 上的动点,求
上的动点,求 到直线
到直线 距离的最小值,并求出此时
距离的最小值,并求出此时 点的坐标.
点的坐标.