(本小题满分10分)选修4-4:坐标系与参数方程
已知直线 的参数方程为
的参数方程为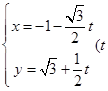 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,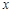 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆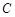 的极坐标方程为
的极坐标方程为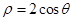 .
.
(Ⅰ)求圆 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设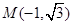 ,直线
,直线 与圆
与圆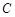 相交于点
相交于点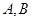 ,求
,求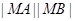 .
.
取一根长度为3m的绳子,拉直后在任意位置剪断,则剪得的两段的长度都不小于1m的概率有多大?
一海豚在水池中自由游弋。水池为长30m、宽20 m的长方形。求此刻海豚嘴尖离岸边不超过2m的概率。
平面上画了一些彼此相距2a的平行线,把一枚半径r<a的硬币任意掷在这平面上,求硬币不与任一条平行线相碰的概率。
取一个边长为2a的正方形及其内切圆,随机向正方形内丢一粒豆子,求豆子落入圆内的概率。
街道旁边有一游戏:在铺满边长为9cm的正方形塑料板的宽广地面上,掷一枚半径为1cm的小圆板,规则如下:每掷一次交5角钱,若小圆板压在边上,可重掷一次;若掷在正方形内,需再交5角钱可玩一次;若掷在或压在塑料板的顶点上,可获得一元钱,试问:
(1)小圆板压在塑料板的边上的概率是多少?
(2)小圆板压在塑料板顶点上的概率是多少?