(本小题满分12分)设函数 .
.
(1)若函数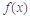 在
在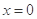 处有极值,求函数
处有极值,求函数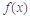 的最大值;
的最大值;
(2)①是否存在实数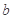 ,使得关于
,使得关于 的不等式
的不等式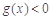 在
在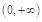 上恒成立?若存在,求出
上恒成立?若存在,求出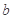 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
②证明:不等式
某学生社团在对本校学生学习方法开展问卷调查的过程中发现,在回收上来的1000份有效问卷中,同学们背英语单词的时间安排共有两种:白天背和晚上临睡前背.为研究背单词时间安排对记忆效果的影响,该社团以5%的比例对这1000名学生按时间安排类型进行分层抽样,并完成一项实验,实验方法是,使两组学生记忆40个无意义音节(如XIQ、GEH),均要求在刚能全部记清时就停止识记,并在8小时后进行记忆测验.不同的是,甲组同学识记结束后一直不睡觉,8小时后测验;乙组同学识记停止后立刻睡觉,8小时后叫醒测验.
两组同学识记停止8小时后的准确回忆(保持)情况如图(区间含左端点而不含右端点)
(1)估计1000名被调查的学生中识记停止后8小时40个音节的保持率大于等于60%的人数;
(2)从乙组准确回忆因结束在[12,24)范围内的学生中随机选3人,记能准确回忆20个以上(含20)的人数为随机变量X,求X分布列及数学期望;
(3)从本次实验的结果来看,上述两种时间安排方法中哪种方法背英语单词记忆效果更好? 计算并说明理由.
在ΔABC中,角A、B、C所对的边分别为a,b,c,且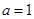 ,
, ,
,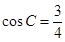 .
.
(1)求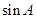 的值;
的值;
(2)求ΔABC的面积.
已知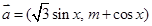 ,
,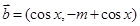 , 且
, 且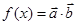 .
.
(1) 求函数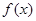 的解析式;
的解析式;
(2) 当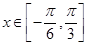 时,
时, 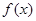 的最小值是-4 , 求此时函数
的最小值是-4 , 求此时函数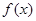 的最大值, 并求出相应的
的最大值, 并求出相应的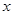 的值.
的值.
(满分14分)某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60) ...[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 从成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.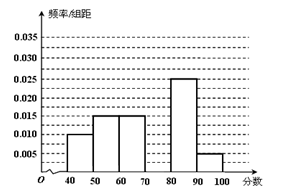
一纸箱中放有除颜色外,其余完全相同的黑球和白球,其中黑球2个,白球3个.
(Ⅰ)从中同时摸出两个球,求两球颜色恰好相同的概率;
(Ⅱ)从中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.