如图,A(0,1),M(3,2),N(4,4) , 动点P从点A出发,沿y
轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为 t 秒.(直线y = kx+b平移时k不变)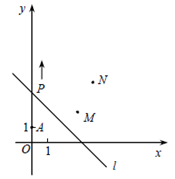
(1)当t=3时,求 l 的解析式;
(2)若点M,N位于l 的异侧,确定 t 的取值范围.
已知 ,
, ,
, (如图).
(如图). 是射线
是射线 上的动点(点
上的动点(点 与点
与点 不重合),
不重合), 是线段
是线段 的中点.
的中点.
(1)设 ,
, 的面积为
的面积为 ,求
,求 关于
关于 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(2)如果以线段 为直径的圆与以线段
为直径的圆与以线段 为
为 直径的圆外切,求线段
直径的圆外切,求线段 的长;
的长;
(3)连结 ,交线段
,交线段 于点
于点 ,如果以
,如果以 为顶点的三角形与
为顶点的三角形与 相似,求线段
相似,求线段 的长.
的长.
某电子科技公司开发一种新产品.产品投产上市一年来,公司经历了由
初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次).公司
前12个月累积获得的利润y(万元)与销售时间第x(月)之间的函数关系(即前x个月的
利润总和y与x之间的关系)对应的点都在如图所示的图 象上.该图象是某二次函数
象上.该图象是某二次函数
y=a(x-h)2+k图象的一部分,点A为抛物线的顶点,且点A,B,C的横坐标分别为4,10,
12,点A,B的纵 坐标分别为-16,20.
坐标分别为-16,20.
(1)求前12个月该公司累积获得的利润y(万元)与时间第x(月)之间的函数关系式;
(2)分别求出前9个月公司累积获得的利润和10月份一个月内所获得的利润;
(3)在前12个月中,哪个月该公司一个月内所获得的利润最多?最多利润是多少万元?
在平面上有且只有4个点,这4个点中有一个独特的性质:连结每两点可得到6条线段,这6条线段有且只有两种长度.我们把这四个点称作准等距点.例如正方形ABCD的四个顶点(如图1),有AB=BC=CD=DA,AC=BD.其实满足这样性质的图形有很多,如图2中A、B、C、O四个点,满足AB=BC=CA,OA=OB=OC;如图3中A、B、C、O四个点,满足OA=OB=OC=BC,AB=AC.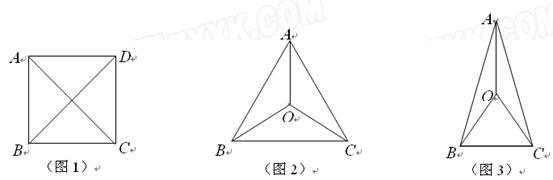
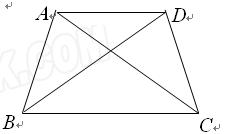
(1)如图,若等腰梯形ABCD的四个顶点是准等距点,且AD∥BC.
①写出相等的线段(不再添加字母);
②求∠BCD的度数.
(2)请再画出一个四边形,使它的四个顶点为准等距点,并写出相等的线段.
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸
货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图
所示.解答下列问题: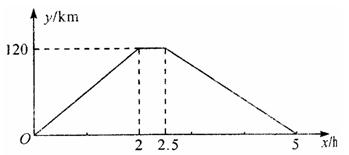
(1)这辆汽 车的往、返速度是否相同?请说明理由;
车的往、返速度是否相同?请说明理由;
(2)求这辆汽车从甲地出发4h时与甲地的距离.
函数 的图象如图所示.
的图象如图所示.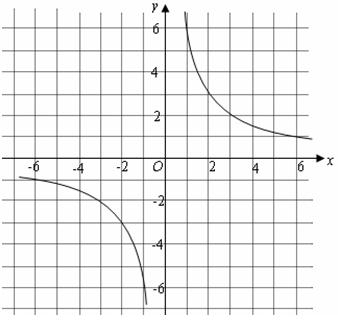
(1) (
(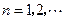 )是第一象限内图象上的点,且
)是第一象限内图象上的点,且 都是整数.求出所有的点
都是整数.求出所有的点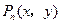 ;
;
(2)若P(m,y1),Q(-3,y2)是函数 图象上的两点,且y1> y2,求实数m的取值范围.
图象上的两点,且y1> y2,求实数m的取值范围.