如图1，对于平面上不大于
的∠MON，我们给出如下定义：若点P在∠MON的内部或边界上，作PE⊥OM于点E，PF⊥ON于点F，则称PE+PF为点P相对于∠MON的“点角距离”，记为
．
如图2，在平面直角坐标系xOy中，对于
，点P为第一象限内或两条坐标轴正半轴上的动点，且满足
5，点P运动形成的图形记为图形G．
（1）满足条件的其中一个点P的坐标是 ，图形G与坐标轴围成图形的面积等于 ；
（2）设图形G与x轴的公共点为点A，已知
，
，求
的值；
（3）如果抛物线
经过（2）中的A，B两点，点Q在A，B两点之间的抛物线上（点Q可与A，B两点重合），求当
取最大值时，点Q 的坐标．
阅读以下材料：
对于实数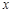
、
、
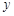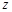定义两种新运算，规定
表示这三个数的平均数，
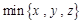表示这三个数中最小的数，例如：
；
．
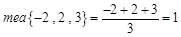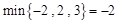（1）求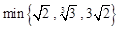
的值；
（2）已知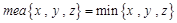
对于任意实数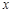、、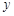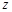都成立，则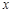、、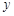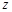应满足怎样的关系式？
（3）已知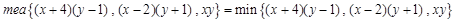
，求
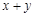的值．
图①是一个长为
、宽为
的长方形，用这样四个全等的长方形，拼成如图②的正方形．
（1）按要求填空：
ⅰ．请用含字母、的代数式表示图②中的阴影部分的正方形的边长： ；
ⅱ．请用含字母、的代数式，用两种不同的方法表示图②中阴影部分的面积：
方法1：
方法2：
ⅲ．观察图②，请写出代数式
、
、
之间的等量关系： ；
（2）根据（1）题中的等量关系，解决如下问题：
若
，
，求
的值．
先化简，再求值：
，其中
，
满足
．
（1）解方程：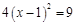
（2）分解因式：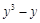
数学思想运用：
（1）如图①所示，△ABC的外角平分线交于G，若∠A=80°，则∠BGC= °，请你猜测∠BGC和∠A的数量关系： ．
（2）如图②所示，若△ABC的内角平分线交于点I，若∠A=50°，则∠BIC= °，请你猜测∠BIC和∠A的数量关系： ．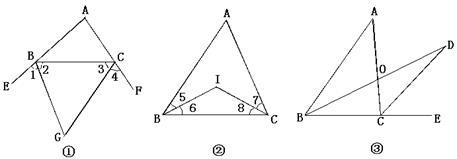
（3）已知，如图③，△ABC中，
的平分线与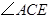
的平分线交于
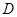点，请你猜测∠D和∠A的数量关系： ．
若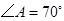
，求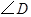
的度数（写出求解过程）．