（1）观察发现
如图（1）：若点A、B在直线m同侧，在直线m上找一点P，使AP+BP的值最小，做法如下：
作点B关于直线m的对称点B′，连接AB′，与直线m的交点就是所求的点P，线段AB′的长度即为AP+BP的最小值．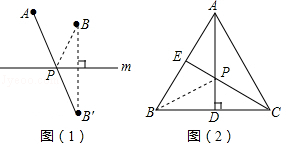
如图（2）：在等边三角形ABC中，AB=2，点E是AB的中点，AD是高，在AD上找一点P，使BP+PE的值最小，做法如下：
作点B关于AD的对称点，恰好与点C重合，连接CE交AD于一点，则这点就是所求的点P，故BP+PE的最小值为 ．
（2）实践运用
如图（3）：已知⊙O的直径CD为2，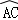
的度数为60°，点B是
的中点，在直径CD上作出点P，使BP+AP的值最小，则BP+AP的值最小，求BP+AP的最小值．
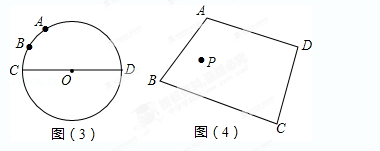
（3）拓展延伸
如图（4）：点P是四边形ABCD内一点，分别在边AB、BC上作出点M，点N，使△PMN的周长最小，保留作图痕迹，不写作法．
已知，如图，在四边形ABCD中，AB∥CD，E，F为对角线AC上两点，且AE=CF，DF∥BE，AC平分∠BAD．求证：四边形ABCD为菱形．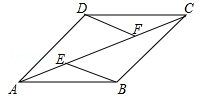
先化简，再求值：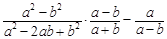
，其中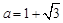
，
．
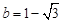如图，在平面直角坐标系
中，直线
与
轴交于点
，与
轴交于点
．抛物线
的对称轴是
且经过
、
两点，与
轴的另一交点为点
．
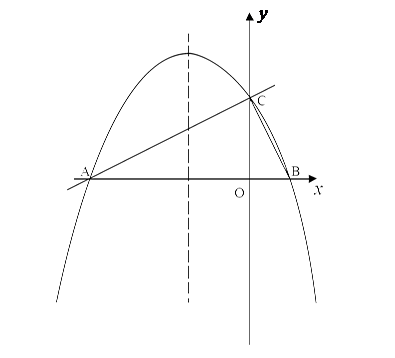
（1）①直接写出点
的坐标；②求抛物线解析式．
（2）若点
为直线
上方的抛物线上的一点，连接
．求
的面积的最大值，并求出此时点
的坐标．
（3）抛物线上是否存在点
，过点
作
垂直
轴于点
，使得以点
、
、
为顶点的三角形与
相似？若存在，求出点
的坐标；若不存在，请说明理由．
鄂州市化工材料经销公司购进一种化工原料若干千克，价格为每千 克30元．物价部门规定其销售单价不高于每千克60元，不低于每千克30元．经市场调查发现：日销售量y（千克）是销售单价x（元）的一次函数，且当x=60时 ，y=80；x=50时，y=100．在销售过程中，每天还要支付其他费用450元．
（1）求出y与x的函数关系式，并写出自变量x的取值范围．
（2）求该公司销售该原料日获利w（元）与销售单价x（元）之间的函数关系式．
（3）当销售单价为多少元时，该公司日获利最大？最大获利是多少元？
如图，在△ABC中，AB=AC，AE是∠BAC的平分线，∠ABC的平分线 BM交AE于点M，点O在AB上，以点O为圆心，OB的长为半径的圆经过点M，交BC于点G，交 AB于点F．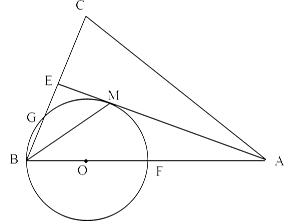
（1）求证：AE为⊙O的切线．
（2）当BC=8，AC=12时，求⊙O的半径．
（3）在（2）的条件下，求线段BG的长．