如图是一个半圆形湖面景点的平面示意图.已知 为直径,且
为直径,且 km,
km, 为圆心,
为圆心,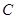 为圆周上靠近
为圆周上靠近 的一点,
的一点, 为圆周上靠近
为圆周上靠近 的一点,且
的一点,且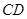 ∥
∥ .现在准备从
.现在准备从 经过
经过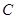 到
到 建造一条观光路线,其中
建造一条观光路线,其中 到
到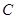 是圆弧
是圆弧 ,
,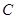 到
到 是线段
是线段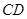 .设
.设 ,观光路线总长为
,观光路线总长为 .
.
(1)求 关于
关于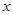 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.
(13分)在 的对边,已知
的对边,已知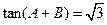 ,
, ,又△ABC的面积
,又△ABC的面积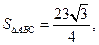
(1)求cosC的值;
(2)求△ABC的周长。
(13分)三棱锥P-ABC中,三条棱PC.AC.BC两两垂直,长都等于2,M为PA的中点,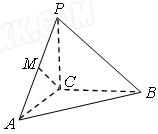
(1)求异面直线CM与AB所成角θ的余弦值;
(2)过点M作一个与平面ABC平行的平面
 ,将此三棱锥截成两部分,分别求这两部分的体积
,将此三棱锥截成两部分,分别求这两部分的体积
(13分)在直角△ABC中AB=4,BC=3,AC=5,将此三角形绕AB边所在直线旋转一周得到一个圆锥
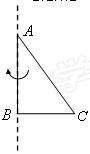
(1)求圆锥的侧面积和体积;
(2)求这个圆锥的内切球的表面积。
海面上相距10海里的A.B两船,B船在A船的北偏东45°方向上,两船同时接到指令同时驶向C岛,C岛在B船的南偏东75°方向上,行驶了80分钟后两船同时到达C岛,经测算,A船行驶了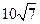 海里,求B船每小时的速度。
海里,求B船每小时的速度。
(本小题满分16分)已知数列
 ,其中数列
,其中数列 是首项为2公比为
是首项为2公比为 的等比数列,又
的等比数列,又 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求使不等式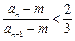 成立的所有正整数
成立的所有正整数 的值.
的值.