某校组织七年级学生参加社会实践活动,如果单独租用45座客车若干辆,则刚好坐满;如果单独租用60座客车,则可少租1辆,并且剩余15个座位.
(1)该校参加社会实践活动有多少人?
(2)已知45座客车的日租金为每辆1000元,60座客车的日租金为每辆1200元,该校租用哪种车更合算?
某市体育中考自选项目有乒乓球、篮球和羽毛球,每个考生任选一项作为自选考试项目.
(1)求考生小红和小强自选项目相同的概率;
(2)除自选项目之外,长跑和掷实心球为必考项目.小红和小强的体育中考各项成绩(百分制)的统计图表如下:

|
考生 |
自选项目 |
长跑 |
掷实心球 |
|
小红 |
95 |
90 |
95 |
|
小强 |
90 |
95 |
95 |
①补全条形统计图.
②如果体育中考按自选项目占 、长跑占 、掷实心球占 计算成绩(百分制),分别计算小红和小强的体育中考成绩.
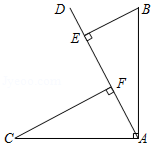
如图, , 是 内部一条射线,若 , 于点 , 于点 .求证: .
先化简,再求值: ,其中 .
如图,在平面直角坐标系 中,抛物线 与两坐标轴分别相交于 , , 三点.
(1)求证: ;
(2)点 是第一象限内该抛物线上的动点,过点 作 轴的垂线交 于点 ,交 轴于点 .
①求 的最大值;
②点 是 的中点,若以点 , , 为顶点的三角形与 相似,求点 的坐标.

如图, 是 的内接三角形,过点 作 的切线交 的延长线于点 , 是 的直径,连接 .
(1)求证: ;
(2)若 , 于点 , , ,求 的值.
