如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4)C(-2,6)
(1)画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1
(2)以原点O为位似中心,画出将△A1B1C1三条边放大为原来的2倍后的△A2B2C2.
在 中, , , 是 的中点. 为直线 上一动点,连接 ,过点 作 ,交直线 于点 ,连接 .

( 1 )如图 1 ,当 是线段 的中点时,设 , ,求 的长(用含 的式子表示);
( 2 )当点 在线段 的延长线上时,依题意补全图 2 ,用等式表示线段 , , 之间的数量关系,并证明.
在平面直角坐标系 中, 为抛物线 上任意两点,其中 .
(1)若抛物线的对称轴为 ,当 为何值时,
(2)设抛物线的对称轴为 .若对于 ,都有 ,求 的取值范围.
小云统计了自己所住小区 5 月 1 日至 30 日的厨余垃圾分出量(单位:千克),相关信息如下:
.小云所住小区 5 月 1 日至 30 日的厨余垃圾分出量统计图:

.小云所住小区 5 月 1 日至 30 日分时段的厨余垃圾分出量的平均数如下:

( 1 )该小区 5 月 1 日至 30 日的厨余垃圾分出量的平均数约为 (结果取整数)
( 2 )已知该小区 4 月的厨余垃圾分出量的平均数为 ,则该小区 5 月 1 日至 30 日的厨余垃圾分出量的平均数约为 4 月的 倍(结果保留小数点后一位);
( 3 )记该小区 5 月 1 日至 10 日的厨余垃圾分出量的方差为 5 月 11 日至 20 日的厨余垃圾分出量的方差为 , 5 月 21 日至 30 日的厨余垃圾分出量的方差为 .直接写出 的大小关系.
小云在学习过程中遇到一个函数 .下面是小云对其探究的过程,请补充完整:
( 1 )当 时,对于函数 ,即 ,当 时, 随 的增大而 ,且 ;对于函数 ,当 时, 随 的增大而 ,且 ;结合上述分析,进一步探究发现,对于函数 ,当 时, 随 的增大而 .
( 2 )当 时,对于函数 ,当 时, 与 的几组对应值如下表:
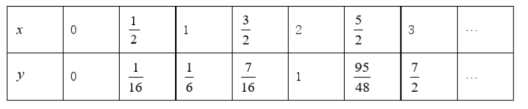
综合上表,进一步探究发现,当 时, 随 的增大而增大.在平面直角坐标系 中,画出当 时的函数 的图象.

( 3 )过点 ( )作平行于 轴的直线 ,结合( 1 )( 2 )的分析,解决问题:若直线 与函数 的图象有两个交点,则 的最大值是 .
如图, 为 的直径, 为 延长线上一点, 是 的切线, 为切点, 于点 ,交 于点 .

( 1 )求证: ;
( 2 )若 , ,求 的长.