如图，二次函数y＝－x2＋nx＋n2－9（n为常数）的图像经过坐标原点和x轴上另一点A，顶点在第一象限．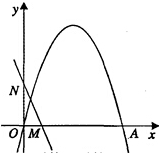
(1)求n的值和点A坐标；
(2)已知一次函数y＝－2x＋b(b >0)分别交x轴、y轴于M、N两点．点P是二次函数图像的y轴右侧部分上的一个动点，若PN⊥NM于N点，且△PMN与△OMN相似，求点P坐标．
因式分解（每题4分，共24分）
（1）
；
（2）
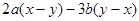
（3）
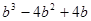
（4）（x＋y）2＋2（x＋y）＋1．
（5）（m2＋n2）2－4m2n2
（6）
先化简，再求值（本题8分）：（4ab3－8a2b2）÷4ab＋（2a＋b）（2a－b），其中a＝2，b＝1．
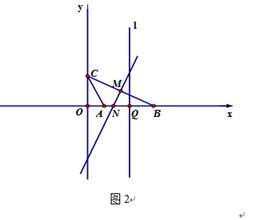
已知：如图1，在△ABC中，A、B、C的坐标分别为（1,0），（4,0），（0,2），点M为边BC上的中点，点N为边AB 上一点，且N的横坐标为方程2n２＋5n－12＝0一个根，
（1）求N的坐标和直线MN的解析式 ；（3+3）
（2）判断直线MN与BC的位置关系，并说明你的理由；（1+3）
（3）如图2，①在图2中作出△ABC的外接圆；②过Q（
，0）作直线
⊥x轴，点P在直线上，且在第一象限，试确定一个点P，使得∠CPB+∠CAB=180°，求出满足条件的P点坐标．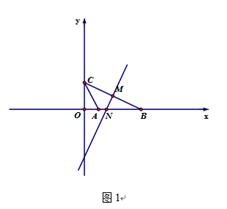
为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等．设BC的长度为xm，矩形区域ABCD的面积为ym2．
（1）求AE的长（用x的代数式表示）
（2）当y=108m2时，求x的值
如图，已知△ABC内接于⊙O，AD、AE分别平分∠BAC和△BAC的外角∠BAF，且分别交圆于点D、E．连接DE，CD，DE与BC相交于点G．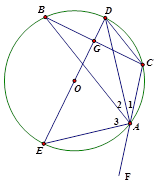
（1）求证：DE是△ABC的外接圆的直径．
（2）设OG=3，CD=2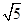
，求⊙O的半径．