如图，已知AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠EAC=∠D=60°. 
（1）求∠ABC的度数；
（2）求证：AE是⊙O的切线；
（3）当BC=4时，求劣弧AC的长．
（本题共8分）已知关于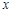
的方程
．
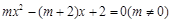（1）求证：方程总有两个实数根；
（2）若方程的两个实数根都是整数，求正整数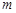
的值．
（本题6分）如图，已知∠AOB，OA=OB,点E在OB上，且四边形AEBF是平行四边形，请你只用无刻度的直尺在图中画出∠AOB的平分线（保留画图痕迹，不写画法），并说明理由．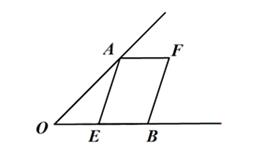
（本题8分）甲、乙两人在5次打靶测试中命中的环数如下：
甲：8，8，7，8，9
乙：5，9，7，10，9
（1）填写下表：
| 平均数 |
众数 |
中位数 |
方差 |
|
| 甲 |
8 |
8 |
||
| 乙 |
9 |
3．2 |
（2）教练根据这5次成绩，选择甲参加射击比赛，教练的理由是什么？
（3）如果乙再射击1次，命中8环，那么乙的射击成绩的方差．（填“变大”、“变小”或“不变”）．
（本小题6分）当a＝2－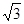
，b＝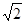
时，求代数式a2＋b2－4a＋2015的值．
（每小题4分，共8分）解方程
（1）
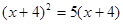
（2）（x－2）（x－5）=－3