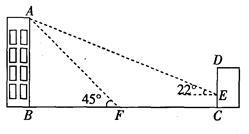
如图，某校教学楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，教学楼在建筑物的墙上留下高2m的影子CE；而当光线与地面的夹角是45°时，教学楼顶A在地面上的影子F与墙角C有13m的距离（B、F、C在一条直线上）．求教学楼AB的高度．
（参考数据：sin22°≈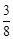
，cos22°≈
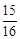，tan22°≈
）
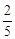（1）画出△ABC关于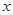
轴对称的图形△A1B1C1，并指出△A1B1C1的顶点坐标.
（2）画出△A1B1C1关于y轴对称的图形△A2B2C2，并指出△A2B2C2的顶点坐标.
如图所示，△ABC为等腰三角形，AB=AC且AD⊥BC，垂足为D，求证：△ABD≌△ACD。
如图，已知AB=AC，∠ABE=∠ACD，BE与CD相交于O，求证：△ABE≌△ACD.
如图，AB=DF，AC=DE，BE=FC，求证：△ABC≌△DFE．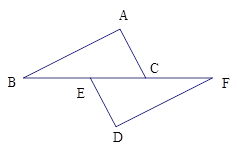
如图所示，AC∥EF，AC=EF，AE=BD.求证：△ABC≌△EDF。（请将下列证明过程补充完整）
证明：∵AC∥EF
∴_______________________（两直线平行，同位角相等）
∵AE=BD
∴AE+EB=EB+BD
∴AB=____________
在△ABC和△EDF中
AC=EF
_______________
AB=___________
∴△ABC≌△EDF（_________）