已知椭圆 (
(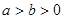 )的离心率为
)的离心率为 ,且满足右焦点
,且满足右焦点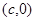 到直线
到直线 的距离为
的距离为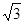 ,
,
(Ⅰ)求椭圆的方程;
(Ⅱ)已知 ,过原点且斜率为
,过原点且斜率为 的直线
的直线 与椭圆交于
与椭圆交于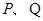 两点,求
两点,求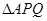 面积的最大值。
面积的最大值。
在棱长为a的正方体ABCD—A′B′C′D′中,E、F分别是BC、A′D′的中点.
求证:四边形B′EDF是菱形;
若函数
(Ⅰ)求函数 的单调区间
的单调区间
(Ⅱ)若对所有的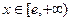 都有
都有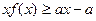 成立,求实数a的取值范围
成立,求实数a的取值范围
为了了解某地区中学甲流防控情况,拟采用分层抽样的方法从A,B,C三个县市中抽取7所中学进行调查,已知A,B,C三个市中分别有36,54,36所中学。
(Ⅰ)求从A,B,C三市中分别抽取的中学数量;
(Ⅱ)若从抽取的7所学校中随机抽取2所进行调查结果的对比,计算这2所学校中至少有1所来自A市的概率。
在△ABC中,a,b,c分别为角A、B、C的对边,设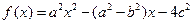
(1) =0且B-C=
=0且B-C=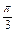 ,求角C的大小;
,求角C的大小;
(2)若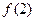 =0,求角C的取值范围.
=0,求角C的取值范围.
已知函数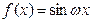 (
( ).
).
(1)当 时,写出由
时,写出由 的图象向右平移
的图象向右平移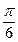 个单位长度得到的图象所对应的
个单位长度得到的图象所对应的
函数解析式;
(2)若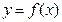 图象过
图象过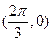 点,且在区间
点,且在区间 上是增函数,求
上是增函数,求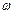 的值.
的值.