(本小题满分14分)
已知函数 在点
在点 处的切线为
处的切线为 .
.
(1)求实数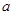 ,
,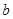 的值;
的值;
(2)是否存在实数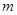 ,当
,当 时,函数
时,函数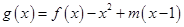 的最小值为
的最小值为 ,若存在,求出
,若存在,求出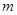 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)若 ,求证:
,求证: .
.
如图,圆O与圆O′内切于点T,点P为外圆O上任意一点,PM与内圆O′切于点M.求证:PM∶PT为定值.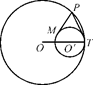
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于D.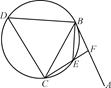
(1)证明:DB=DC;
(2)设圆的半径为1,BC=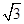 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
如图,AB和BC分别与圆O相切于点D、C,AC经过圆心O,且BC=2OC.求证:AC=2AD.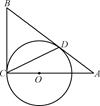
如图,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,求DE的长.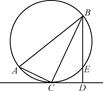
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2,求BC的值.