某公司生产的某批产品的销售量 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用 万元满足
万元满足 (其中
(其中 为正常数).已知生产该批产品还要投入成本
为正常数).已知生产该批产品还要投入成本 万元(不包含促销费用),产品的销售价格定为
万元(不包含促销费用),产品的销售价格定为 元/件.
元/件.
(1)将该产品的利润 万元表示为促销费用
万元表示为促销费用 万元的函数;
万元的函数;
(2)当促销费用投入多少万元时,该公司的利润最大?
数列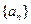 满足:
满足: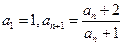
(I)求证: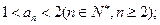
(Ⅱ)令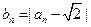
(1)求证: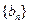 是递减数列;(2)设
是递减数列;(2)设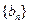 的前
的前 项和为
项和为 求证:
求证:
在一次考试中共有8道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的.评分标准规定:“每题只选一个选项,选对得5分,不选或选错得0分”.某考生已确定有4道题答案是正确的,其余题中:有两道只能分别判断2个选项是错误的,有一道仅能判断1个选项是错误的,还有一道因不理解题意只好乱猜,求:
(1)该考生得40分的概率;
(2)该考生得多少分的可能性最大?

如图,长方体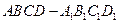 中,
中,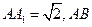
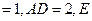 为
为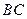 的中点
的中点
(1)求点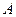 到面
到面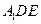 的距离;
的距离;
(2)设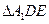 的重心为
的重心为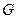 ,问是否存在实数
,问是否存在实数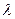 ,使
,使
得 且
且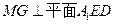 同时成立?若存
同时成立?若存
在,求出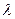 的值;若不存在,说明理由。
的值;若不存在,说明理由。
已知向量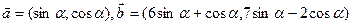 ,设函数
,设函数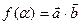 .
.
(Ⅰ)求函数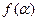 的最大值;
的最大值;
(Ⅱ)在锐角三角形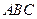 中,角
中,角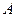 、
、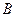 、
、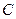 的对边分别为
的对边分别为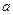 、
、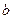 、
、 ,
,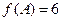 , 且
, 且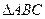 的面积为
的面积为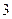 ,
,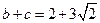
 ,求
,求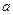 的值.
的值.
已知 两点在抛物线
两点在抛物线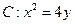 上,点
上,点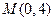 满足
满足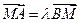
(I)求证: ;
;
(Ⅱ)设抛物线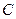 过
过 两点的切线交于点
两点的切线交于点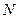
(1)求证:点N在一定直线上;
(2)设 ,求直线
,求直线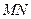 在
在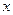 轴上截距的取值范围。
轴上截距的取值范围。