已知椭圆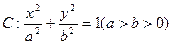 ,其相应于焦点
,其相应于焦点 的准线方
的准线方
程是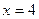 ;
;
(1)求椭圆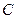 的方程;
的方程;
(2)已知过点 倾斜角为
倾斜角为 的直线交椭圆
的直线交椭圆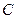 于
于 两点,求弦
两点,求弦 的长度。
的长度。
(3)过点 作两条互相垂直的直线分别交椭圆
作两条互相垂直的直线分别交椭圆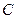 于点
于点 和
和 ,求
,求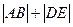
的最小值
已知函数
(1)判断函数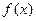 在区间
在区间
上的单调性;(2)若当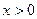 时,
时, 恒成立,求正整数
恒成立,求正整数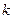 的最大值。
的最大值。
体育课进行篮球投篮达标测试。规定:每位同学有5次投篮机会,若
投中3次则“达标”;为节省时间,同时规定:若投篮不到5次已达标,则停止投篮;若即
便后面投篮全中,也不能达标(前3次投中0次)则也停止投篮。同学甲投篮命中率是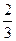 ,
,
且每次投篮互不影响。
(1)求同学甲测试达标的概率;
(2)设测试同学甲投篮次数记为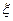 ,求
,求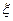 的分布列及数学期望
的分布列及数学期望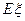 。
。
在三棱锥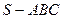 中,侧面
中,侧面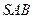 与侧面
与侧面 均是边长为
均是边长为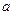 的正
的正
三角形,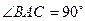 ,
,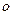 是
是 的中点,
的中点,
(1)求证: 平面
平面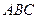 ;
;
(2)求二面角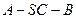 的余弦值
的余弦值
已知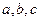 是
是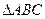 的三个内角
的三个内角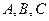 的对边,向量
的对边,向量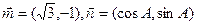 ,若
,若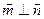 且
且 ,求角
,求角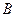 的大小。
的大小。