为了了解某工业园中员工的颈椎疾病与工作性质是否有关,在工业园内随机的对其中50名工作人员是否患有颈椎疾病进行了抽样调查,得到如下的列联表.
| |
患有颈椎疾病 |
没有患颈椎疾病 |
合计 |
| 白领 |
|
5 |
|
| 蓝领 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全部50人中随机抽取1人,抽到患有颈椎疾病的人的概率为 .
.
(1)请将上面的列联表补充完整,并判断是否有99.5%的把握认为患颈椎疾病与工作性质有关?说明你的理由;
(2)已知在患有颈椎疾病的10名蓝领中,有3为工龄在15年以上,现在从患有颈椎疾病的10名蓝领中,选出3人进行工龄的调查,记选出工龄在15年以上的人数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
参考公式: ,其中
,其中 .
.
下面的临界值表仅供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
在一次游戏中,获胜者可得到3件不同的奖品,这些奖品要从已编号的300种不同奖品中随机抽取确定,用系统抽样法确定某获胜者所得到的3件奖品的编号.
某社区的常住人口中,有成年人3200人,其中有无业人员1000人,从事个体劳动的有1160人,有固定收入的上班人员1040人,如果想通过调查其中160人的生活消费情况来了解本社区群众的生活消费情况,考虑到由于各种人员情况的差异,而同一阶层人员的差异较小,问应当采取怎样的抽取方法?从事个体劳动的人员中应抽查多少人?在本问题的设计中还有哪些重要因素将影响调查效果?应怎样改进抽查方案使效果更加客观?
一批车床中有甲厂生产的56台,乙厂生产的42台,用分层抽样法从中抽取14台车床,请写出过程.
已知函数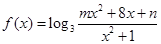 的定义域为
的定义域为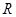 ,值域为
,值域为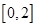 ,求
,求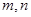 的值。
的值。
已知函数 ,
,
(1)求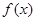 的定义域;
的定义域;
(2)判断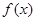 的奇偶性。
的奇偶性。