(本题共8分)如图,抛物线y=-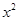 +5x+n经过点A(1,0),与y轴交于点B
+5x+n经过点A(1,0),与y轴交于点B
(1)、求抛物线的解析式;
(2)、P是y轴上一点,且△PAB是以AB为腰的等腰三角形,求P点坐标。
(年广西南宁10分)在平面直角坐标系中, 抛物线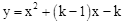 与直线
与直线 交于A, B两点,点A在点B的左侧.
交于A, B两点,点A在点B的左侧.
(1)如图1,当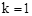 时,直接写出A,B两点的坐标;
时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线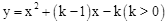 与x轴交于C,D两点(点C在点D的左侧).在直线
与x轴交于C,D两点(点C在点D的左侧).在直线 上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.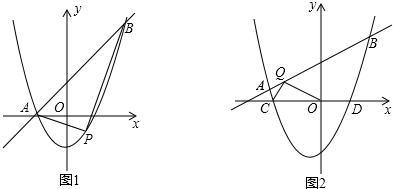
(2014年广东珠海9分)如图,矩形OABC的顶点A(2, 0)、C(0,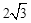 ).将矩形OABC绕点O逆时针旋转30°,得矩形OEFG,线段GE、FO相交于点H,平行于y轴的直线MN分别交线段GF、GH、GO和x轴于点M、P、N、D,连结MH.
).将矩形OABC绕点O逆时针旋转30°,得矩形OEFG,线段GE、FO相交于点H,平行于y轴的直线MN分别交线段GF、GH、GO和x轴于点M、P、N、D,连结MH.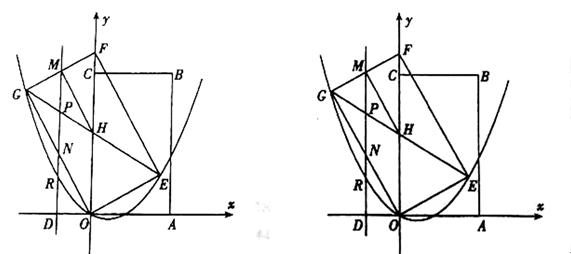
(1)若抛物线 经过G、O、E三点,则它的解析式为: ;
经过G、O、E三点,则它的解析式为: ;
(2)如果四边形OHMN为平行四边形,求点D的坐标;
(3)在(1)(2)的条件下,直线MN抛物线l交于点R,动点Q在抛物线l上且在R、E两点之间(不含点R、E)运动,设ΔPQH的面积为s,当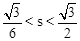 时,确定点Q的横坐标的取值范围.
时,确定点Q的横坐标的取值范围.
(年甘肃兰州12分)如图,抛物线 与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).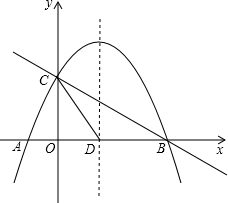
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
如图,在Rt△ABC中,∠ACB=900,AC= ,BC=3,△DEF是边长为a(a为小于3的常数)的等边三角形,将△DEF沿AC方向平移,使点D在线段AC上,DE∥AB,设△DEF与△ABC重叠部分的周长为T。
,BC=3,△DEF是边长为a(a为小于3的常数)的等边三角形,将△DEF沿AC方向平移,使点D在线段AC上,DE∥AB,设△DEF与△ABC重叠部分的周长为T。
(1)求证:点E到AC的距离为一常数;
(2)若AD=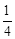 ,当a=2时,求T的值;
,当a=2时,求T的值;
(3)若点D运动到AC的中点处,请用含a的代数式表示T。
(年四川资阳12分)如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;
(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S.