如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形AB-CD的边AB上的“强相似点”,解决问题:
(1)如图①,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由:
(2)如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(3)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.
某工厂设计了一款产品,成本价为每件20元.投放市场进行试销,得到如下数据:
售价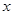 (元∕件) (元∕件) |
…… |
30 |
40 |
50 |
60 |
…… |
日销售量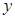 (件) (件) |
…… |
500 |
400 |
300 |
200 |
…… |
(I)若日销售量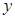 (件)是售价
(件)是售价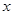 (元∕件)的一次函数,求这个一次函数解析式;
(元∕件)的一次函数,求这个一次函数解析式;
(II)设这个工厂试销该产品每天获得的利润(利润=销售价-成本价)为W(元),当售价定为每件多少元时,工厂每天获得的利润最大?最大利润是多少元?
如图,在一次课外数学实践活动中,小明站在操场的A处,他的两侧分别是旗杆CD和一幢教学楼EF,点A、D、F在同一直线上,从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°,已知DF=14m,EF=15m,求旗杆CD高.(结果精确到0.01m,参考数据: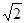 ≈ 1.414,
≈ 1.414, ≈ 1.732)
≈ 1.732)
如图, 是
是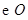 的直径,点
的直径,点 在
在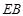 的延长线上,弦
的延长线上,弦 垂足为
垂足为 ,连接
,连接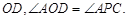
(I)求证: 是
是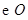 的切线;
的切线;
(II)若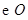 半径为4,
半径为4, 求
求 的长.
的长.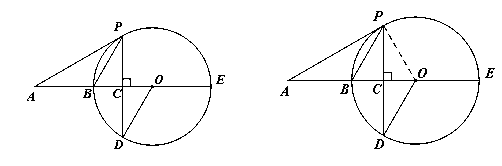
已知一次函数 (b为常数)的图象与反比例函数
(b为常数)的图象与反比例函数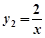 的图象相交于点P(1,a).
的图象相交于点P(1,a).
(I) 求a的值及一次函数的解析式;
(II) 当x>1时,试判断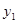 与
与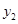 的大小.并说明理由.
的大小.并说明理由.
某小区20户家庭的日用电量(单位:千瓦时)统计如下:
| 日用电量(单位:千瓦时) |
4 |
5 |
6 |
7 |
8 |
10 |
| 户数 |
1 |
2 |
4 |
6 |
5 |
2 |
(I)求这20个样本数据的平均数、众数和中位数;
(II)根据样本数据,估计该小区200户家庭中日均用电量不超过7千瓦时的约有多少户.