(本小题12分)如图,直线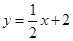 分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥x轴于B,且
分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥x轴于B,且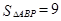 .
.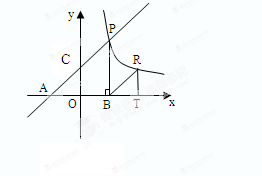
(1)求点P的坐标;
(2)设点R与点P在同一个反比例函数的图象上,且点R在直线PB的右侧,作RT⊥x轴于T,当△BRT与△AOC相似时,求点R的坐标.
科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度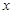 /℃ /℃ |
…… |
-4 |
-2 |
0 |
2 |
4 |
4.5 |
…… |
植物每天高度增长量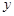 /mm /mm |
…… |
41 |
49 |
49 |
41 |
25 |
19.75 |
…… |
由这些数据,科学家推测出植物每天高度增长量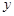 是温度
是温度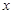 的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由;
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过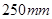 ,那么实验室的温度
,那么实验室的温度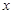 应该在哪个范围内选择?请直接写出结果.
应该在哪个范围内选择?请直接写出结果.
有一座抛物线形拱桥,正常水位时桥下水面宽度为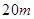 ,拱顶距离水面
,拱顶距离水面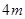 .
.
(1)在如图所示的直角坐标系中,求出该抛物线的解析式;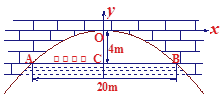
(2)设正常水位时桥下的水深为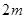 ,为保证过往船只顺利航行,桥下水面的宽度不得小于
,为保证过往船只顺利航行,桥下水面的宽度不得小于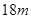 ,求水深超过多少米时就会影响过往船只在桥下的顺利航行.
,求水深超过多少米时就会影响过往船只在桥下的顺利航行.
如图,抛物线与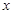 轴交于
轴交于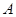 、
、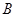 两点,与
两点,与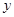 轴交
轴交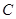 点,点
点,点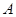 的坐标为
的坐标为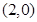 ,点
,点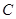 的坐标为
的坐标为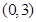 ,它的对称轴是直线
,它的对称轴是直线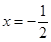 .
.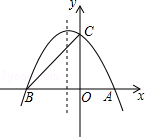
(1)求抛物线的解析式;
(2)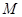 是线段
是线段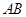 上的任意一点,当
上的任意一点,当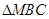 为等腰三角形时,求
为等腰三角形时,求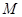 点的坐标.
点的坐标.
如图,已知二次函数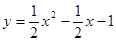 的图象交
的图象交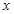 轴于
轴于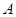 、
、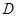 两点.
两点.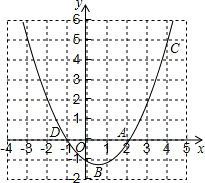
(1)求线段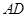 的长;
的长;
(2)在同一坐标系中画出直线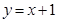 ,并写出当
,并写出当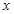 在什么范围内时,一次函数的值大于二次函数的值.
在什么范围内时,一次函数的值大于二次函数的值.
某种盆栽花卉每盆的盈利与每盆种植花卉的株数有关:已知每盆种植3株时,平均每株可盈利4元;若每盆多种植1株,则平均每株盈利要减少0.5元.为使每盆的盈利达到15元,则每盆应种植花卉多少株?