（本小题满分12分）
在平面直角坐标系中，有三个点的坐标分别是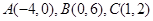
.
（1）证明：A，B，C三点不共线；
（2）求过A，B的中点且与直线
平行的直线方程；
（3）设过C且与AB所在的直线垂直的直线为
，求与两坐标轴围成的三角形的面积.
（本小题满分8分）
已知函数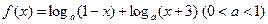
（1）求函数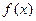
的定义域；
（2）求函数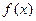的零点；
（3）若函数f(x)的最小值为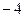
，求
的值.
（本小题满分8分）
计算求值
(1) 
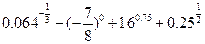
(2) 
（本小题满分8分）
设全集U="{1," 2, 3, 4, 5}, 集合A="{1," a2－1, 4}, 
="{2," a+3}
(I)求a值;
(II)满足AÍBU这样的集合B共有几个?试将这样的B集合都写出来
（文科做）
设集合
，
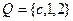，且满足
, 若
．
(Ⅰ) 求b = c的概率；
（Ⅱ）求方程
有实根的概率
(理科做)设函数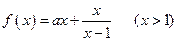
（1）若a>0,求函数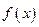
的最小值；
（2）若a是从1，2，3三个数中任取一个数，b是从2，3，4，5四个数中任取一个数，
求f (x)>b恒成立的概率