(本小题满分14分)
设椭圆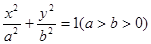 的离心率为
的离心率为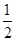 ,其左焦点
,其左焦点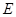 与抛物线
与抛物线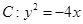 的焦点相同.
的焦点相同.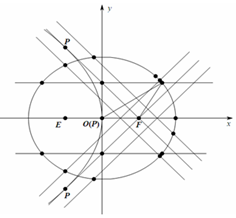
(1)求此椭圆的方程;
(2)若过此椭圆的右焦点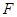 的直线
的直线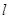 与曲线
与曲线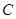 只有一个交点
只有一个交点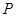 ,则
,则
①求直线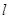 的方程;
的方程;
②椭圆上是否存在点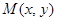 ,使得
,使得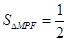 ,若存在,请说明一共有几个点;若不存在,请说明理由.
,若存在,请说明一共有几个点;若不存在,请说明理由.
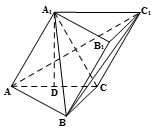
(本题共12分,第(Ⅰ)问6分,第(Ⅱ)问6分)如图所示,已知三棱柱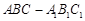 ,点
,点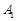 在底面
在底面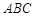 上的射影恰为
上的射影恰为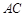 的中点
的中点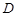 ,
,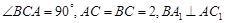 .
.
(Ⅰ)求证: 平面
平面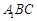 ;
;
(Ⅱ)求二面角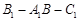 的余弦值.
的余弦值.
(本题共13分,第(Ⅰ)问6分,第(Ⅱ)问7分)已知函数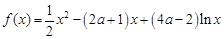
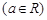 .
.
(Ⅰ)若函数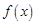 在
在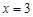 处取得极值,求曲线
处取得极值,求曲线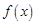 在点
在点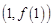 处的切线方程;
处的切线方程;
(Ⅱ)当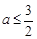 时,讨论
时,讨论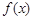 的单调区间.
的单调区间.
(本题共13分,第(Ⅰ)问6分,第(Ⅱ)问7分)
已知向量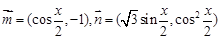 ,函数
,函数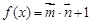 .
.
(Ⅰ)若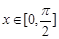 ,
,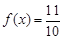 ,求
,求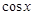 的值;
的值;
(Ⅱ)在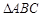 中,角
中,角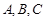 的对边分别是
的对边分别是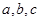 ,且满足
,且满足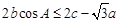 ,求
,求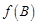 的取值范围.
的取值范围.
(本题共13分,第(Ⅰ)问5分,第(Ⅱ)问8分)
今年3月1日,重庆某中学50位学生参加了“北约联盟”的自主招生考试.这50位同学的数学成绩的频率分布直方图如图所示,其中成绩分组区间是: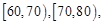
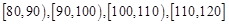 .
.
(Ⅰ)求图中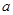 的值;
的值;
(Ⅱ)从成绩不低于100分的学生中随机选取2人,该2人中成绩在110分以上(含110分)的人数记为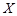 ,求
,求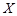 的分布列和数学期望.
的分布列和数学期望.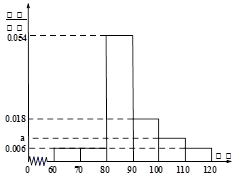
已知函数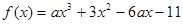 ,
,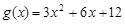 ,和直线m:y=kx+9,又
,和直线m:y=kx+9,又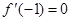 .
.
(1)求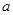 的值;
的值;
(2)是否存在k的值,使直线m既是曲线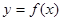 的切线,又是
的切线,又是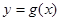 的切线;如果存在,求出k的值;如果不存在,说明理由.
的切线;如果存在,求出k的值;如果不存在,说明理由.
(3)如果对于所有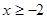 的
的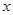 ,都有
,都有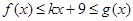 成立,求k的取值范围.
成立,求k的取值范围.