(本小题满分14分)
如图6,已知点 是圆心为
是圆心为 半径为1的半圆弧上从点
半径为1的半圆弧上从点 数起的第一个三等分点,
数起的第一个三等分点, 是直径,
是直径, ,直线
,直线 平面
平面 .
.

(1)证明: ;
;
(2)在 上是否存在一点
上是否存在一点 ,使得
,使得 ∥平面
∥平面 ,若存在,请确定点
,若存在,请确定点 的位置,并证明之;若不存在,请说明理由;
的位置,并证明之;若不存在,请说明理由;
(3)求点 到平面
到平面 的距离.
的距离.
如图,已知离心率为 的椭圆
的椭圆 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线 交椭圆C于不同的两点A、B.
交椭圆C于不同的两点A、B.
(1)求椭圆C的方程.
(2)证明:直线MA、MB与x轴围成一个等腰三角形.
如图,在直三棱柱 中,
中,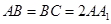 ,
, ,
, 是
是 的中点.
的中点.
(1)求证: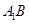 ∥平面
∥平面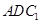 ;
;
(2)求二面角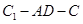 的余弦值;
的余弦值;
(3)试问线段 上是否存在点
上是否存在点 ,使
,使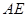 与
与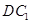 成
成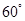 角?若存在,确定
角?若存在,确定 点位置,若不存在,说明理由.
点位置,若不存在,说明理由. 
盒中装有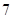 个零件,其中
个零件,其中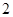 个是使用过的,另外
个是使用过的,另外 个未经使用.
个未经使用.
(1)从盒中每次随机抽取 个零件,每次观察后都将零件放回盒中,求
个零件,每次观察后都将零件放回盒中,求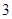 次抽取中恰有
次抽取中恰有 次抽到使用过的零件的概率;
次抽到使用过的零件的概率;
(2)从盒中随机抽取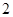 个零件,使用后放回盒中,求此时盒中使用过的零件个数为3或4概率.
个零件,使用后放回盒中,求此时盒中使用过的零件个数为3或4概率.
已知函数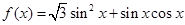 ,
,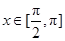 .
.
(1)求方程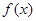 =0的根;
=0的根;
(2)求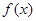 的最大值和最小值.
的最大值和最小值.
已知正项数列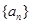 满足:
满足:
(1)求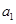 的范围,使得
的范围,使得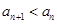 恒成立;
恒成立;
(2)若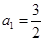 ,证明:
,证明:
(3)若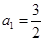 ,证明:
,证明: