已知等差数列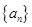 的前n项和为
的前n项和为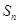 ,满足
,满足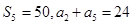 ,
,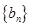 为递增的等比数列,且
为递增的等比数列,且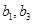 是方程
是方程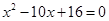 的两个根.
的两个根.
(I)求数列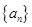 ,
,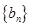 的通项公式;
的通项公式;
(II)若数列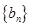 满足
满足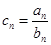 ,求数列
,求数列 的前n项和
的前n项和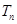 .
.
(本小题满分14分)已知函数 (aÎR).
(aÎR).
(Ⅰ)当a=2时,求函数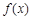 在(1, f(1))处的切线方程;
在(1, f(1))处的切线方程;
(Ⅱ)求函数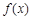 的单调区间;
的单调区间;
(Ⅲ)若函数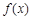 有两个极值点
有两个极值点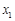 ,
, 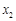 (
(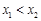 ),不等式
),不等式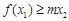 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(本小题满分13分)已知动点P到定点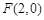 的距离和它到定直线
的距离和它到定直线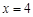 的距离的比值为
的距离的比值为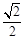 .
.
(Ⅰ)求动点P的轨迹W的方程;
(Ⅱ)若过点F的直线与点P的轨迹W相交于M,N两点(M,N均在y轴右侧),点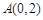 、
、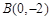 ,设A,B,M,N四点构成的四边形的面积为S,求S的取值范围.
,设A,B,M,N四点构成的四边形的面积为S,求S的取值范围.
(本小题满分12分)如图,三棱柱ABC-A1B1C1中,平面ABB1A1⊥底面ABC,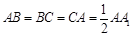 ,∠A1AB=120°,D、E分别是BC、A1C1的中点.
,∠A1AB=120°,D、E分别是BC、A1C1的中点.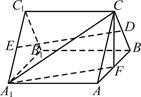
(Ⅰ)试在棱AB上找一点F,使DE∥平面A1CF;
(Ⅱ)在(Ⅰ)的条件下,求二面角A-A1C-F的余弦值.
(本小题满分12分)已知数列{an},{bn}满足:a1b1+a2b2+a3b3+…+anbn=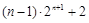 (
( ).
).
(Ⅰ)若{bn }是首项为1,公比为2的等比数列,求数列{an}的前n项和Sn;
(Ⅱ)若{an}是等差数列,且an≠0,问:{bn}是否是等比数列?若是,求{an}和{bn}的通项公式;若不是,请说明理由.
(本小题满分12分)已知向量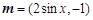 ,
,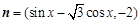 ,函数
,函数 .
.
(Ⅰ)求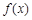 在区间
在区间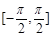 上的零点;
上的零点;
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c, 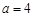 ,△ABC的面积
,△ABC的面积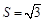 ,当x=A时,函数
,当x=A时,函数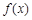 取得极大值,求
取得极大值,求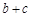 的值.
的值.